1.3 遗传算法-精英保留

精英保留策略

为了防止当前群体的最优个体在下一代发生丢失，导致遗传算法不能收敛到全局最优解，De Jong在其博士论文中提出了精英选择(Elitism)策略，也称为精英保留(Elitist Preservation)策略。把群体在进化过程中迄今出现的最好个体不进行遗传操作而直接复制到下一代中，一般会将其替换下一代中的最劣个体。精英保留策略改进了标准遗传算法的全局收敛能力，并且从理论上被证明了具有精英保留的标准遗传算法是全局收敛的。

以下即在前文标准遗传算法的基础上，采用上一代最优个体替换遗传操作后产生的子代中的随机个体，即将该精英个体无条件复制到子代。

import numpy as np
import copy

1 种群

目前仅考虑浮点数编码，因此省去了编码/解码过程——整个染色体就是解向量，每个基因是其中一个分量。

Individual类表征个体，重要的属性为：

solution 解向量
evaluation 目标函数值
fitness 适应度值

Population类表征群体，根据个体实例生成指定大小的种群，其中：

individuals 所有个体列表，Numpy的ndarray类型
best 最优个体

class Individual:
    def __init__(self, ranges):
        '''
        ranges: element range of solution, e.g. [(lb1, ub1), (lb2, ub2), ...]
        validation of ranges is skipped...
        '''
        self.ranges = np.array(ranges)
        self.dimension = self.ranges.shape[0]

        # 初始化解向量
        seeds = np.random.random(self.dimension)
        lb = self.ranges[:, 0]
        ub = self.ranges[:, 1]
#         print("seeds",seeds)
        self._selution = lb + (ub-lb)*seeds
#         print("self._solution",self._selution)

        # 评估与适应度
        self.evaluation = None
        self.fitness = None

    @property
    def solution(self):
        return self._selution

    @solution.setter
    def solution(self, solution):
        assert self.dimension == solution.shape[0]
        assert (solution>=self.ranges[:,0]).all() and (solution<=self.ranges[:,1]).all()
        self._selution = solution

class Population:
    def __init__(self, individual, size=50):
        '''
        individual: 个体
        size: 个体数量
        '''
        self.individual = individual
        self.size = size
        self.individuals = None

    def initialize(self):
        '''初始化下一代'''
        IndvClass = self.individual.__class__
        self.individuals = np.array([IndvClass(self.individual.ranges) for i in range(self.size)], dtype=IndvClass)

    def best(self, fun_evaluation, fun_fitness=None):
        '''得到最好的个体'''
        _, evaluation = self.fitness(fun_evaluation, fun_fitness)
        pos = np.argmin(evaluation)
        return self.individuals[pos]

    def fitness(self, fun_evaluation, fun_fitness=None):
        '''
        为每个个体计算目标值和适应度
        fun_evaluation: 目标函数 
        fun_fitness: 有估计值计算适应度 
        '''
        if not fun_fitness:
            fun_fitness = lambda x:x 

        evaluation = np.array([fun_evaluation(I.solution) if I.evaluation is None else I.evaluation for I in self.individuals])
#         print(evaluation.shape)

        fitness = fun_fitness(evaluation)
        fitness /= np.sum(fitness)
#         print(fitness.shape)

        for I,e,f in zip(self.individuals, evaluation, fitness):
            I.evaluation = e 
            I.fitness = f 

        return fitness, evaluation

2 遗传算子

2.1 选择

采用标准的轮盘赌（RouletteWheel）方式，以种群中个体的适应度为参考，从中选择出同样大小的新的种群个体。从上一节种群适应度的计算可知，个体的适应度已经被归一化，因此可以直接作为轮盘赌的概率参考。

#=====================选择==========================
class Selection:
    '''选择操作的基类'''
    def select(self, population, fitness):
        raise NotImplementedError

class RouletteWheelSelection(Selection):
    '''
    用轮盘赌选择群体  
    群体中使用适应度函数选择个体 
    '''
    def select(self, population, fitness):
        selected_individuals = np.random.choice(population.individuals, population.size, p=fitness)

        population.individuals = np.array([copy.deepcopy(I) for I in selected_individuals])

交叉

从选择后的样本中随机选择两个个体a和b，以一定的概率进行交叉操作：将随机位置的对应基因（例如 $g_a$ ， $g_b$ ）按系数 $\alpha$ 进行线性插值，其余位置保持不变，从而得到两个新的个体a'和b'。

对于交叉位置的基因：

$g_a' = g_a + (g_b-g_a)(1-\alpha)$

$g_b' = g_b - (g_b-g_a)(1-\alpha)$

对于非交叉位置的基因：

$g_a' = g_a$

$g_b' = g_b$

综合起来，个体a和b所有位置的基因交叉操作可以写成向量形式：

$a' = a+(b-a)(1-\alpha)\beta$

$b' = b-(b-a)(1-\alpha)\beta$

其中， $\beta$ 表示是否进行交叉的0-1向量。

自适应交叉概率

本文采用的自适应策略为根据参与交叉操作的两个个体a、b的适应度 $f_a, f_b$ 调整交叉概率：适应度越大交叉概率越小，反之同理。首先设定交叉概率区间 $[P_{min}, P_{max}]$ ，然后计算种群个体适应度 $f_i$ ，及平均适应度 $f_{avg}$ 、最大适应度 $f_{max}$ ，那么交叉概率 $P$ 由下式确定：

$P = P_{max}\,\,\,(f < f_{avg})$

$P = P_{max} - (P_{max}-P_{min}) \frac{f-f_{avg}}{f_{max}-f_{avg}} \,\,\,(f \geq f_{avg})$

其中， $f=max(f_a, f_b)$ 为参与交叉操作的两个个体中适应度较大者。

得益于之前程序的非耦合性，只需修改Crossover类即可。

#=====================交叉==========================
class Crossover:
    def __init__(self, rate=0.8, alpha=0.5):
        '''
        rate: 交叉概率 
        alpha: '''
        self.rate = rate
        self.alpha = alpha

    @staticmethod
    def cross_individuals(individual_a, individual_b, alpha):
        '''交叉操作
        alpha: 线性插值银因子，当alpha=0.0， 两个基因焦交换
        '''
        pos = np.random.rand(individual_a.dimension) <= 0.5

        temp = (individual_b.solution - individual_a.solution)*pos * (1-alpha)
        new_value_a = individual_a.solution + temp
        new_value_b = individual_b.solution - temp

        new_individual_a = Individual(individual_a.ranges)
        new_individual_b = Individual(individual_b.ranges)

        new_individual_a.solution = new_value_a
        new_individual_b.solution = new_value_b

        return new_individual_a, new_individual_b

    def cross(self, population):
        adaptive = isinstance(self.rate, list)
        if adaptive:
            fitness = [I.fitness for I in population.individuals]
            fit_max, fit_avg = np.max(fitness), np.mean(fitness)

        new_individuals = []
        random_population = np.random.permutation(population.individuals)
        num = int(population.size/2.0)+1

        for individual_a,individual_b in zip(population.individuals[0:num+1], random_population[0:num+1]):
            if adaptive:
                fit = max(individual_a.fitness, individual_b.fitness)
                if fit_max-fit_avg:
                    i_rate = self.rate[1] if fit<fit_avg else self.rate[1]-(self.rate[1]-self.rate[0])*(fit-fit_avg)/(fit_max-fit_avg)
                else:
                    i_rate = (self.rate[0]+self.rate[1])/2.0
            else:
                i_rate = self.rate

            if np.random.rand() <= i_rate:
                child_individuals = self.cross_individuals(individual_a, individual_b, self.alpha)
                new_individuals.extend(child_individuals)
            else: 
                new_individuals.append(individual_a)
                new_individuals.append(individual_b)

        population.individuals = np.array(new_individuals[0: population.size+1])
#         print(population.individuals)

2.3变异

浮点数编码个体的变异操作为将随即位置的基因g增加或减少一个随机值。这个随机值由允许变化区间乘以一个[0,1]区间的随机数 $\alpha$ 来确定。例如基因g的区间为[L,U]，则变异后的基因g'：

$g=g-(g-L)\alpha , (rand()<=0.5)$

$g=g+(U-g)\alpha , (rand()>=0.5)$

#=====================变异==========================
class Mutation:
    def __init__(self, rate):
        self.rate = rate

    def mutate_individual(self, individual, positions, alpha):
        '''
        positions: 变异位置， list 
        alpha： 变异量
        '''
        for pos in positions:
            if np.random.rand() < 0.5:
                individual.solution[pos] -= (individual.solution[pos]-individual.ranges[:,0][pos])*alpha
            else:
                individual.solution[pos] += (individual.ranges[:,1][pos]-individual.solution[pos])*alpha

        individual.evaluation = None
        individual.fitness = None

    def mutate(self, population, alpha):
        '''alpha： 变异量'''
        for individual in population.individuals:
            if np.random.rand() > self.rate:
                continue
#             print(individual)
            num = np.random.randint(individual.dimension)+1
            pos = np.random.choice(individual.dimension, num, replace=False)
            self.mutate_individual(individual, pos, alpha)

3. 遗传算法

本次实现的遗传算法默认求最小值，因此适应度函数应为目标函数值的反函数。并且考虑到它将作为选择概率，即函数值应非负。于是，此处设置为如下形式：

$f(x) = arctan(-x) + \pi$

3.1变异度自适应

前文的变异操作由变异概率和变异程度（下式中的 $\alpha$ ）共同决定：

$g = g - (g-L)\alpha\,\,\,(rand() \leq 0.5)$

$g = g + (U-g)\alpha\,\,\,(rand()>0.5)$

为了使种群在进化的后期趋于稳定，应减小变异作用。相应措施为减小变异概率或者变异程度，本文采用与进化代数负相关的变异程度值，即设置 $\alpha$ 与进化代数 $n$ ，总代数 $N$ 的关系为：

3.2 精英保留策略

以下即在前文标准遗传算法的基础上，采用上一代最优个体替换遗传操作后产生的子代中的随机个体，即将该精英个体无条件复制到子代。

相应地，仅需修改GA模块遗传算法类GA的run()函数：

class GA:
    def __init__(self, population, selection, crossover, mutation, fun_fitness=None):
        self.population = population
        self.selection = selection
        self.crossover = crossover
        self.mutation = mutation
        self.fun_fitness = fun_fitness if fun_fitness else (lambda x:np.arctan(-x)+np.pi)

    def run(self, fun_evaluation, gen=50, elitism=True):
        self.population.initialize()

        for n in range(1, gen+1):
            if elitism:
                the_best = copy.deepcopy(self.population.best(fun_evaluation, self.fun_fitness))

            fitness, _ = self.population.fitness(fun_evaluation, self.fun_fitness)

            self.selection.select(self.population, fitness)

            self.crossover.cross(self.population)

#             self.mutation.mutate(self.population, np.random.rand())
            mutation_rate = 1.0 - np.random.rand()**(1.0-n/gen)
            self.mutation.mutate(self.population, mutation_rate)

            if elitism:
                pos = np.random.randint(self.population.size)
                self.population.individuals[pos] = the_best


        return self.population.best(fun_evaluation, self.fun_fitness)

4 测试

采用二元函数Schaffer_N4进行测试，最小值点 $f(0,1.25313)=0.292579$ 。

$f(x,y) = 0.5+\frac{cos^2 [sin(|x^2-y^2|)] - 0.5}{[1+0.001(x^2+y^2)]^2} , (-10<=(x,y)<=10)$

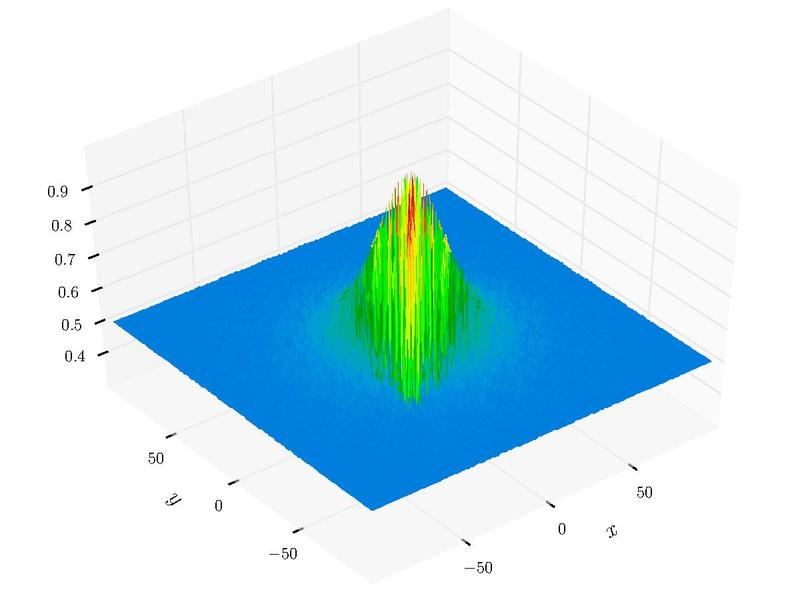
schaffer_n4 = lambda x: 0.5 + (np.cos(np.sin(abs(x[0]**2-x[1]**2)))**2-0.5) / (1.0+0.001*(x[0]**2+x[1]**2))**2  

I = Individual([(-10,10)]*2)
P = Population(I, 50)
S = RouletteWheelSelection()
# C = Crossover(0.9, 0.75)
C = Crossover([0.5,0.9], 0.75)

M = Mutation(0.2)
g = GA(P, S, C, M)

res = []
for i in range(10):
    res.append(g.run(schaffer_n4, 500).evaluation)

val = schaffer_n4([0,1.25313])
val_ga = sum(res)/len(res)

print('the minimum: {0}'.format(val))
print('the GA minimum: {0}'.format(val_ga))
print('error: %.3f%%' % ((val_ga/val-1.0)*100))

the minimum: 0.29257863204552975
the GA minimum: 0.29258691877301246
error: 0.003%

10.3 遗传算法-精英保留