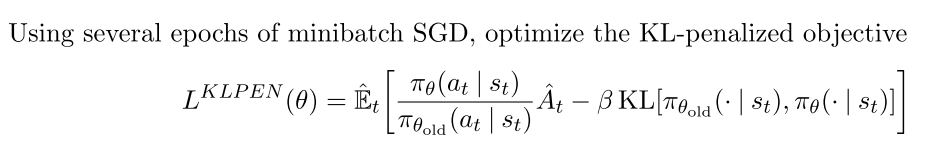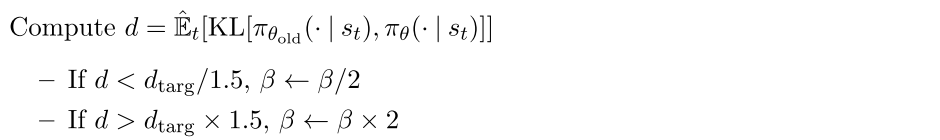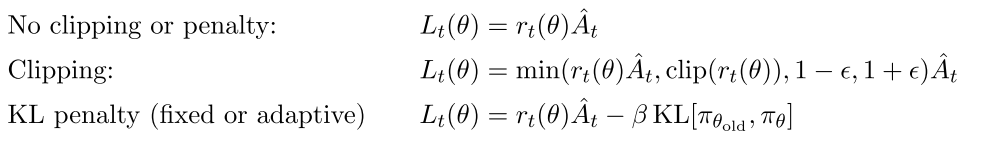0.3 强化学习-PPO

paper:Proximal Policy Optimization Algorithms

核心:

on-policy策略梯度算法, 使用重要性采样解决从行动策略进行采样的问题, 但是与off-policy算法不同, 这里的行动策略是老策略 $\theta_{old}$ , 所以还是相当于on-policy算法.
TRPO算法的改进版, 把 $\beta KL(\theta, \theta')$ 添加进目标函数里, 一阶优化算法, 更容易实现, 样本复杂度也更高, (而TRPO作为最优化算法的约束项, 而且不使用策略梯度).
交替执行从策略中采样数据和代理("surrogate")目标函数优化过程, 优化时进行minibatch的多epochs更新. 而标准PG算法每抽样一次数据进行一次梯度更新.
该算法的样本复杂度(越复杂越好), 算法复杂度(越简单越好), 挂钟时间(越短越好) 具有很好的平衡.
cliped的目标函数代表了策略得下界, 使用TD(n)计算优势函数 $A$ .

1. 背景

1.1. PG

策略梯度算法一般是把策略梯度喂进随机梯度上升算法里, 常用梯度估计器为

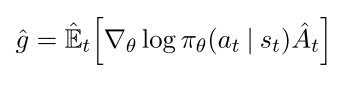	(1)

其中 $\pi_\theta$ 为随机策略, $\hat{A}_t$ 为优势函数. 计算该梯度, 一般要构造目标函数为

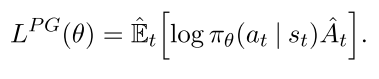	(2)

该函数不适合用同一个trajectory做多步优化, 往往效果很差.

1.2. Trust Region Methods

TRPO算法的优化过程改为一个到约束最优化过程, 其约束限制策略更新的幅度,

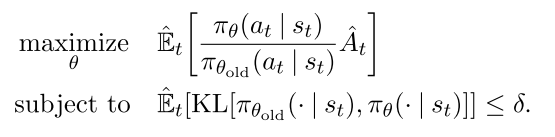	(3, 4)

其中, $\theta_{old}$ 是更新前的策略参数向量. 对目标进行线性逼近, 对约束进行二次逼近, 该问题可用共轭梯度算法有效地近似求解.

PPO算法把约束项作为惩罚项, 将上述问题变为无约束问题,

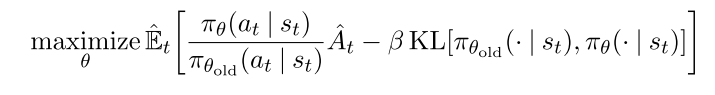	(5)

其中 $\beta$ 需要自适应修改, 优势函数需要增加一些约束.

2. PPO

2.1 Clipped Surrogate Objective (PPO2)

令 $r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ , 因此 $r(\theta_{old})=1$ , TRPO最大化目标函数:

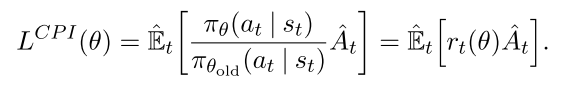	(6)

上标CPI表示保守策略迭代(conservative policy iteration [KL02]). 如果不加约束直接优化上述L会造成策略更新太大, 因此要考虑如何惩罚策略更新幅度, 让它不太远离1. 构造如下目标函数,

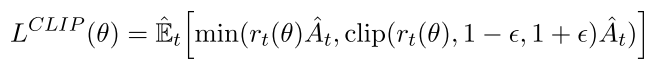	(7)

加clip的意思是


fig 1


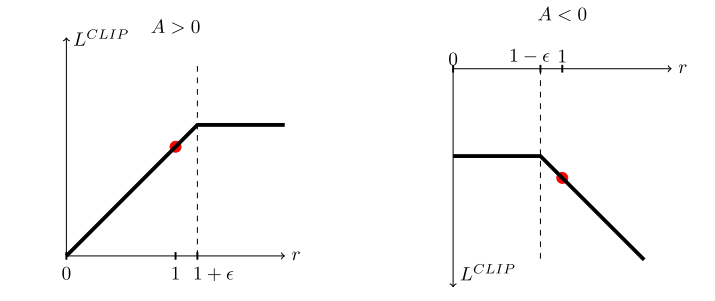fig

2.2. Adaptive KL Penalty Coefficient (PPo1)

另一种解决思路是自适应惩罚因子 $\beta$ , 该算法在每次策略更新中执行下面两步:

更新后的 $\beta$ 用于下一次策略更新.

2.3. 多步更新计算A

有很多方法计算方差减少的优势函数(variance-reduced advantage-function estimators).

广义优势函数如下:

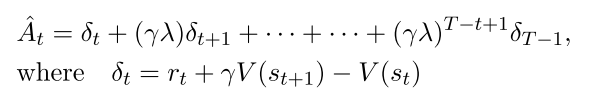	(11, 12)

本文使用广义优势函数的截断版本, 令 $\lambda=1$ , 得,

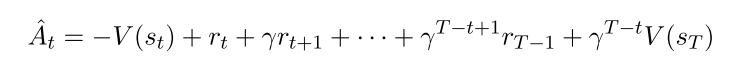	(10)

2.4 PPO算法伪代码

通过构造 $L^{CLIP}$ 或者 $L^{KLPEN}$ 的损失函数可以直接用自动微分进行多步SGD优化.

整体损失函数为

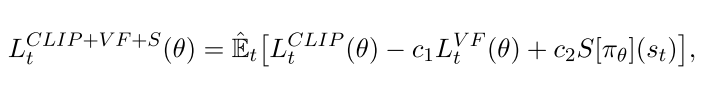	(9)

其中, $c_1, c_2$ 是系数, $S$ 表示an entropy bonus, $L_t^{VF}$ 表示均方误差损失, $(V_\theta(s_t) - V_t^{targ})^2$ , 一般 $V_t^{targ} \leftrightarrow \hat{R_t}$

PPO算法使用固定长度trajectory片段, 每次迭代中, 每N个并行Actor收集T个时间步得数据, 然后使用这NT个数据构造代理目标损失函数, 并使用K个epochs的minibatch-SGD优化该损失函数, 通常Adam算法表现比较好.


fig 2

3. 实验

3.1 实验设置

测试的损失函数
对于KL散度版本, 可以使用固定或自适应的 $\beta$ , 并使用target KL value $d_{targ}$ . 作者测试了log空间中的版本,但是表现并没有变好.
在7个环境中测试算法, 每个训练100万步, 超参数 $\epsilon, \beta, d_{targ}$ 使用了搜索, 其他的超参数是指定的.
策略表示: 使用2x64的FC层+tanh激活, 输出高斯分布均值, 其标准差可变;
策略函数和值函数不共享参数, 所以参数 $c_1$ 无关, 也不使用entropy bonus项;
每个算法都在7个环境中测试, 使用最后100 episodes的平均总回报作为比较,


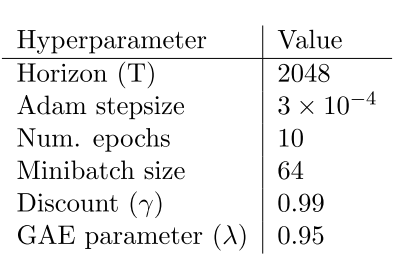Table 3: PPO hyperparameters used for the Mujoco 1 million timestep benchmark

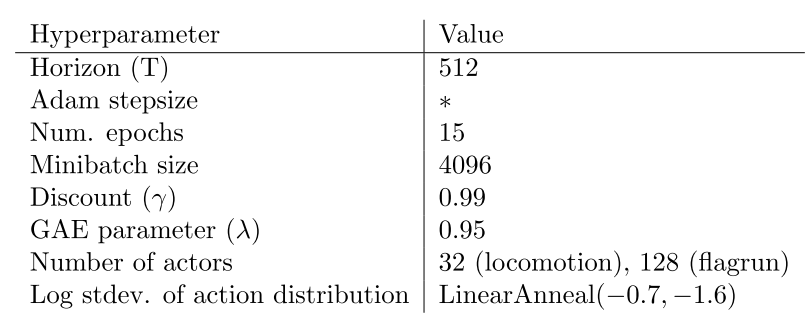Table 4: PPO hyperparameters used for the Roboschool experiments. Adam stepsize was adjusted based on the target value of the KL divergence.

Table 5: PPO hyperparameters used in Atari experiments. α is linearly annealed from 1 to 0 over the course of learning.

讨论

目前RL提高点:

扩展性(大型模型以及并行化)
数据效率
鲁棒性(不用调超参数也可适用于多个任务).

目前主流算法缺点:

DQN, 可解释性差, 不适应连续控制任务
VPG, 数据效率低, 鲁棒性差
TRPO, 算法太复杂, 不适用于存在噪声(dropout)或者参数共享(策略与值函数共享参数, 或任务与辅助任务共享参数)的结构.

PPO简单有效的方法.

0. 强化学习-PPO