7-凸优化

1 基础概念

  • 优化: 从⼀个可⾏解的集合中, 寻找最优的元素
    • 线性规划/非线性规划
    • 凸优化/非凸优化
    • 光滑/非光滑
    • 单目标优化/多目标优化, (多目标优化往往无法同时使得多个目标函数最小，需要进行折中选择， 或者将多个目标进行加权求和)
  • 凸优化: 如果一个问题是凸优化问题, 那么其目标函数是凸函数, 约束为凸集(约束由若干个凸函数组成)
    • 线性规划一定是一个凸规划
名称 英文 定义 解释
过任意两点的直线 f(x)=θx1+(1−θ)x2,θ∈R f({x}) = \theta x_1 + (1 - \theta) x_2 ,\theta \in R
过任意两点的线段 f(x)=θx1+(1−θ)x2,θ∈[0,1] f({x}) = \theta x_1 + (1 - \theta) x_2 ,\theta \in [0,1]
n 维空间的子空间 α,β∈V,k∈R⇒α+β∈V,kα∈V\alpha, \beta\in V, k\in R\Rightarrow \alpha+\beta\in V, k\alpha \in V, 则 V 为RnR^n的子空间 子空间: RnR^n的非空子集 V, 且对加法和数乘运算封闭. 对减法肯定也封闭.
n 维空间的子空间一定包含零向量 (过原点).
过原点的平面或直线, 以原点为起点的所有向量为R3R^3空间的子空间
线性函数 f(αx+βy)=αf(x)+βf(y)f(\alpha x+\beta y) = \alpha f(x)+\beta f(y)
凸函数 f(αx+βy)≤αf(x)+βf(y)f(\alpha x+\beta y) \leq \alpha f(x)+\beta f(y)
名称 英文 定义 解释
仿射集 Affine Sets 一个集合 C 中，连接任意两点的直线也在该集合中，则该集合为仿射集 直线/二维空间都是仿射集; 线段、闭合图形不是仿射集。
仿射组合 affine combination 设集合 C 中的 k 个点, x1,⋯,xk∈C;θ1,⋯,θk∈R,θ+⋯+θk=1x_{1}, \cdots, x_{k} \in C; \theta_{1}, \cdots, \theta_{k} \in \mathbb{R}, \theta+\cdots+\theta_{k}=1, 则θ1x1+⋯+θkxk\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}为 k 个点的仿射组合 若集合 C 中 k 个点的仿射组合也在 C 中, 则 C 为仿射集
仿射包 affine hull  aff C={θ1x1+⋯+θkxk∣x1,…,xk∈C,θ1+⋯+θk=1}\text { aff } C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \ldots, x_{k} \in C, \theta_{1}+\cdots+\theta_{k}=1\right\} 集合 C 中元素的所有仿射组合, (包含集合 C 的最小仿射集)称为 C 的仿射包
与 C 相关的子空间 C 是仿射集,V=C−x0={x−x0∥x∈C},∀x0∈C V = C-x_0 = \{x-x_0 \| x \in C\}, \forall x_0 \in C 该式表示对仿射集 C 的平移, 过原点, 具有更好的性质.
∀V1,V2∈V,∀α,β∈R\forall V_{1}, V_{2} \in V , \forall \alpha, \beta \in \mathbb{R} , 使得 αV1+βV2∈V\alpha V_{1}+\beta V_{2} \in V
凸集 Convex Set C is a Convex Set ⇔∀θx1+(1−θ)x2∈C,x1,x2∈C∀θθ∈[0,1]C \text { is a Convex Set } \Leftrightarrow \forall \theta x_{1}+(1-\theta) x_{2} \in C, x_{1}, x_{2} \in C \forall \theta \quad \theta \in[0,1] 一个集合是凸集，当属于该集合的任意两点之间的线段仍然在该集合内。
仿射集一定是凸集
凸组合 convex combination θ1x1+⋯+θkxk,θ1+⋯+θk=1,θi≥0,i=1,...k\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}, \theta_{1}+\cdots+\theta_{k}=1, \theta_{i} \ge 0, i=1,...k CC 为凸集 ⇔\Leftrightarrow 任意元素凸组合 ∈C \in C
凸包 convex hull ConvC={θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,...k,θ1+⋯+θk=1}Conv C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_i \in C, \theta_i \ge 0, i=1,...k, \theta_{1}+\cdots+\theta_{k}=1\right\} 集合 C (不一定是凸集) 中元素的所有凸组合, (包含集合 C 的最小凸集)称为 C 的凸包
名称 英文 定义 解释
锥 CC 是锥 ⇔∀x∈C,θ≥0\Leftrightarrow \quad \forall x \in C, \theta \geq 0 , 有 θx∈C\theta x \in C 锥一定是过原点的集合
凸锥 Convex Cone CC 是凸锥 ⇔∀x1,x2∈C,θ1,θ2≥0\Leftrightarrow \quad \forall x_{1}, x_{2} \in C, \theta_{1}, \theta_{2} \geq 0 , 有 θ1x1+θ2x2∈C\theta_{1} x_{1}+\theta_{2} x_{2} \in C
锥组合 conic combination θ1x1+⋯+θkxkθ1,⋯,θk≥0\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \quad \theta_{1}, \cdots, \theta_{k} \geq 0
凸锥包 conic hull {θ1x1+⋯+θkxk∣x1,⋯,xk∈C,θ1,⋯,θk≥0}\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \cdots, x_{k} \in C, \theta_{1}, \cdots, \theta_{k} \geq 0\}

比较

名称 比较
仿射组合 ∀θ1,⋯,θk,θ1+⋯+θk=1\forall \theta_{1}, \cdots, \theta_{k}, \quad \theta_{1}+\cdots+\theta_{k}=1
凸组合 ∀θ1,⋯,θkθ1+⋯+θk=1,θ1,⋯,θk>0\forall \theta_{1}, \cdots, \theta_{k} \quad \theta_{1}+\cdots+\theta_{k}=1, \theta_{1}, \cdots, \theta_{k}>0
凸锥组合 ∀θ1,⋯,θkθ1+⋯+θk≥0\forall \theta_{1}, \cdots, \theta_{k} \quad \theta_{1}+\cdots+\theta_{k} \geq 0

几种重要的凸集

  • 仿射集
    • 任意线性方程组的解集都是仿射集
    • 任意一个仿射集, 都可以写成一个线性方程组的解集
    • 与 C 相关的子空间, 性质更好的子空间, 一定是过原点的
  • 仿射集是凸集的一个特例
  • 单个点的集合
    • 一定是仿射集, 凸集
    • 过原点是凸锥, 不过原点不是凸锥集
  • 空集, 是仿射集, 凸集, 凸锥集
  • 直线
    • 一定是仿射集, 凸集
    • 过原点是凸锥, 不过原点不是凸锥集
集合 仿射集 凸集 凸锥集 定义
N 维(RnR^n)空间 √ √ √
RnR^n空间的子空间 √ √ √
任意直线 √ √ (过原点)
任意线段 (点) √ (原点)
(射线) (v=0) √ (x0=0x_0=0) {x0+θv∥θ≥0},x0,v∈Rn,θ∈R\{x_0+\theta v \| \theta\ge 0\}, x_0, v\in R^n, \theta\in R
超平面 √ √ (过原点) {x∣aTx=b}x,a∈Rn,b∈R,a≠0\left\{x \mid a^{T} x=b\right\} \quad x, a \in \mathbb{R}^{n}, b \in \mathbb{R}, a \neq 0
半空间 不是 √ (过原点) 空间中被超平面分割的(≥b,≤b\ge b , \le b)两个部分
集合 仿射集 凸集 凸锥集 定义
球 (欧氏空间) (半径等于 0) √ (原点) B(xc,r)={x∣∥x−xc∥2≤r}={x∣(x−xc)T(x−xc)≤r}B\left(x_{c}, r\right)=\left\{x \mid\left\|x-x_{c}\right\|_{2} \leq r\right\}=\left\{x \mid \sqrt{\left(x-x_{c}\right)^{T}\left(x-x_{c}\right)} \leq r\right\}
椭球 (欧氏空间) (半径等于 0) √ (原点) ε(xc,P)={x∣(x−xc)TP−1(x−xc)≤1}P∈S++n\varepsilon\left(x_{c}, P\right)=\left\{x \mid\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leq 1\right\} \quad P \in S_{++}^{n} (n * n 对称正定矩阵, 奇异值>=0)
P 矩阵的每个特征值对应着椭球一个维度上半径的长度
(此处考虑有界的) 多面体 √ P={x∣ajTx≤bjj=1,⋯,m,cjTx=djj=1,⋯,r}P=\left\{x \mid a_{j}^{T} x \leq b_{j} j=1, \cdots, m, c_{j}^{T} x=d_{j} j=1, \cdots, r\right\}
(本质是一些超平面和半空间的交集)
可能是没有界的
单纯形（Simplex） √ 单纯形是一种特殊的多面体.
定义看笔记 P8
-- -- -- -- --
对称矩阵集合 √ √ Sn={x∈Rn∗n∣x=xT}S^{n}=\left\{x \in \mathbb{R}^{n * n} \mid x=x^{T}\right\}
对称半正定矩阵集合 √ √ S+n={x∈Rn∗n∣x=xT,x⪰0}S_{+}^{n}=\left\{x \in \mathbb{R}^{n * n} \mid x=x^{T}, x \succeq 0\right\}
对称正定矩阵集合 × S++n={x∈Rn∗n∣x=xT,x≻0}S_{++}^{n}=\left\{x \in \mathbb{R}^{n * n} \mid x=x^{T}, x \succ 0\right\}
如何证明不是凸锥?
令 n=1, 则 S+n=R+,S++n=R++,Sn=RS_{+}^{n}=\mathbb{R}_{+}, S_{++}^{n}=\mathbb{R}_{++} , S^{n}=\mathbb{R}, 正定矩阵不含 0 矩阵, 因此不是凸锥
  • {x∣x≤0}\{x \mid x \leq 0\}是凸集，是多面体, 是单纯形
    • 单纯形证明, 取x0=0,x1=−∞x_{0}=0, x_{1}=-\infty

保凸变换

  • (多个)凸集的交集
  • 仿射变换
    • 线性变换和仿射函数的区别.(f(x)=Ax // f(x)=Ax+b)
    • 仿射变换逆运算也是保凸变换
    • 椭球是球的仿射变换
    • 缩放和移位
  • 凸集的和
  • 线性矩阵不等式（LMI）
    • 线性矩阵不等式的解集是凸集
  • 透视函数
    • 任意凸集的反透视映射也是凸集
  • 线性分数函数
    • 先进行仿射变换, 在进行透视变换, 是一种非线性变换
  • 两个随机变量的联合概率 --(映射)--> 条件概率
    • 两个随机变量的联合概率是凸集
    • 其实是贝叶斯公式

3 凸函数

f 是凸函数, -f 是凹函数 大于号的时候严格凸

定义

定义(1)
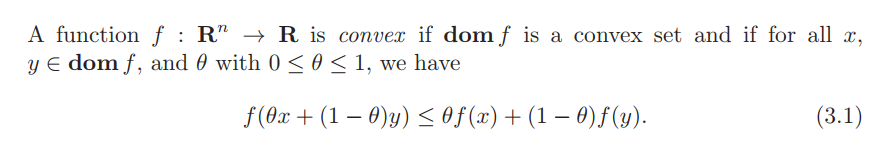
定义(2)

f is convex if and only if for all x∈domfx \in \mathbf{dom} f and all v, the function g(t)=f(x+tv)g(t) = f(x + tv) is convex (on its domain, {t∣x+tv∈domf}\{t | x + tv \in \mathbf{dom} f\}).

  • 通过把函数限制在一条直线上, 验证是否是凸的
定义(3) 一阶条件
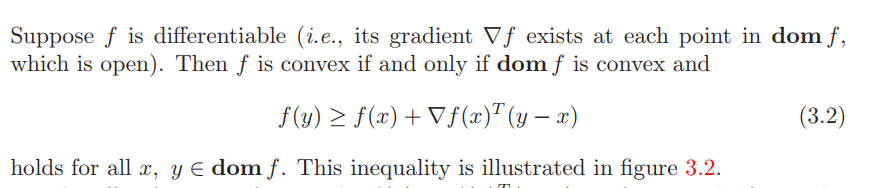
  • f 的定义域一定是一个开集, 因为如果是闭集的话在边界上不可微
  • 切线在 y 处的值一定小于函数值
定义(4) 二阶条件

一阶偏导单调不减

重要的凸函数

  • 示性函数 (分情况讨论)
    • 不在定义域的函数值为无穷或无定义时, 是凸的
    • 如果不在定义域的的函数值为具体值时, 不是凸的
  • 二次函数
    • 二阶导 f′′(x)=Pf''(x) = P, 讨论 P 的(半)正(负)定, 得凹凸性
  • f(x)=1/(x2),x≠0,x∈Rf(x) = 1/(x^2), x\ne 0, x\in R
    • 不是凸函数, 定义域不是凸集
  • 仿射函数
    • 既是凸的又是凹的
  • 指数函数
    • 是凸函数, f(x)=eax,x∈Rf(x)=e^{ax}, x\in R
  • 幂函数, 分情况讨论
    • f(x)=xa,x∈R++f(x)=x^{a}, x \in \mathbb{R}_{++}
    • ∇2f(x){≥0a≥1 or a≤0 – convex≤00≤a≤1 – concave=0a=0 or a=1 – concave and convex  \nabla^{2} f(x)\left\{\begin{array}{ll} \geq 0 & a \geq 1 \text{ or } a \leq 0 \text{ -- convex}\\ \leq 0 & 0 \leq a \leq 1 \text{ -- concave}\\ = 0 & a=0 \text{ or } a=1 \text{ -- concave and convex } \end{array}\right.
  • 绝对值的幂函数 (分情况讨论, P16)
  • 对数函数 -- 严格凹函数
  • 负熵 -- 严格凸函数
  • RnR^n空间的范数 P(x),x∈RnP(x), x \in R^n
  • 空间范数, 是凸函数
  • 零范数-不是范数
    • 非零元素数目（不是凸函数）
  • 极大值函数, 或者极小极大函数-- 凸函数
    • maxf(x)max f(x)
    • minx  maxyf(x,y)min_x \ \ max_y f(x,y)
  • 解析逼近(log-sum-exp), 凸函数
    • 因为极大(极小)函数不可微, 所以可以通过解析逼近分析
  • 几何平均, (所有元素相乘再开 n 次根) -凹函数
  • 对称半正定矩阵的行列式的对数 (分情况讨论) -- 凹函数

保凸运算

  • 非负加权和(积分)
  • 仿射映射
    • 先对变量仿射变换, 再经过 f, 是凸函数
    • 变量不变, 对 f 进行仿射变换, A 如果非负, 是凸函数
  • 两个函数的极⼤值函数
create By cicoa            此页面修订于： 2022-06-28 03:15:43

results matching ""

    No results matching ""