2 spinup-PG

代码:github spinup-PG

1. 策略梯度导出

首先考虑参数化的随机策略$\pi_\theta$, 我们的目标是基于该策略最大化期望奖励 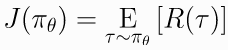, 使用梯度上升算法优化策略.

(1)

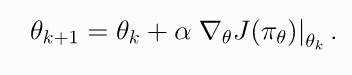
策略性能函数的梯度 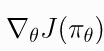称为策略梯度. 一般PG算法需要两个步骤: 1) 导出策略performance的梯度, 表示成期望值的形式; 2) 构造期望值的抽样估计函数.

首先介绍几个概念:

1. Probability of a Trajectory.

(2)

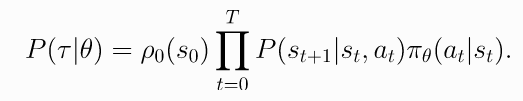
1. The Log-Derivative Trick.

(3)

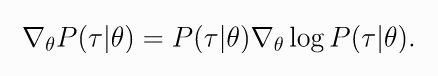
1. Log-Probability of a Trajectory.

(4)

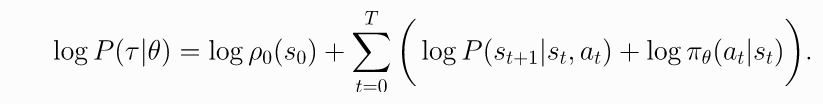
1. Gradients of Environment Functions. 环境动力学方程不依赖于参数$\theta$, 所以,$\rho_0(s_0), P(s_{t+1}|s_t, a_t), R(\tau)$的梯度为0.

2. Grad-Log-Prob of a Trajectory.

(5)

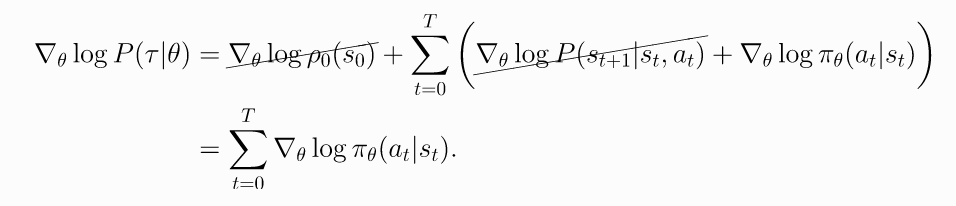
由此,

导出策略梯度

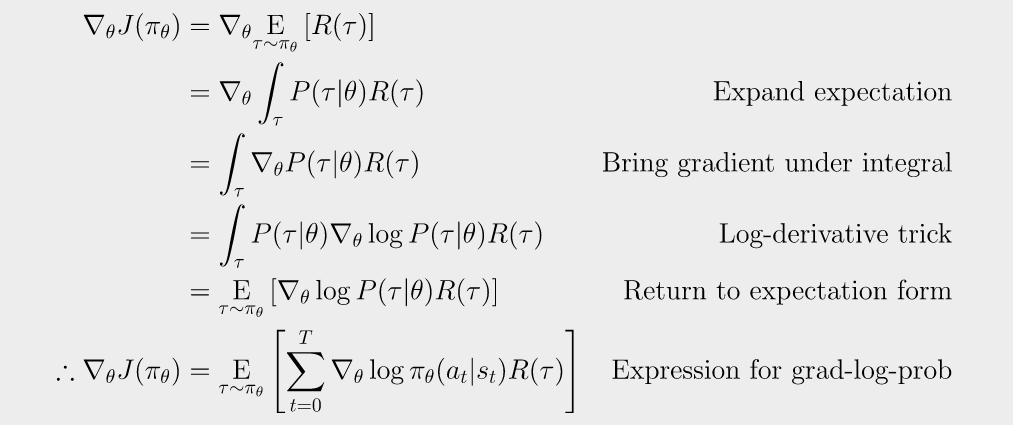
因此策略梯度可以表示成期望的形式, 可以使用样本均值来估计. 通过策略$\pi_\theta$从环境中获取轨迹$\mathcal{D} = \{\tau_i\}_{i=1, ..., N}$, 则策略梯度估计值为

(6)

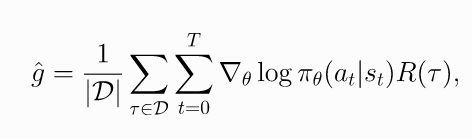
2. 代码

代码: github

==这里说明上述loss的问题是为了警示: 在监督学习里关注loss下降, 模型表现变好, 但是在策略梯度里, 关注loss下降是没有意义的, 只需要关注平均回报.==

3. Expected Grad-Log-Prob Lemma

这一节导出一个常用的中间结果. 称为期望log梯度概率引理(Expected Grad-Log-Prob, EGLP lemma).

EGLP Lemma假设$P_{\theta}$是随机变量$x$上的一个参数化概率分布, 那么

(7)

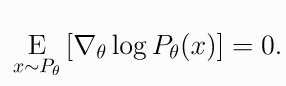
证明

Proof

4. 去除之前状态的影响--降低方差

上一步的策略梯度为

(8)

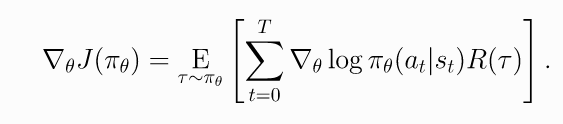
这个公式考虑了所有步骤的奖励, 包括当前状态之前的奖励. 按理说不应该考虑, 所以上式可以变化为

(9)

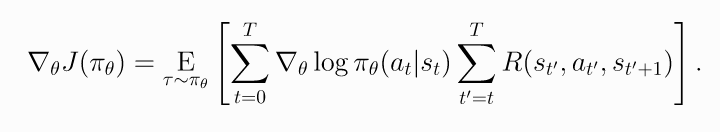
上式称为"reward-to-go policy gradient".

为什么去掉之前时间步的奖励会变好呢? 策略梯度的一个关键问题是使用多少trajectory样本得到其低方差估计. 上述公式(8)的均值为0 但是包含非零方差, 因此这些样本在策略梯度的估计中添加了噪声. 通过去掉这些没用的reward, 减少了噪声, 可以减少所需的样本数量.

这本质也是解决了不同动作的信用分配问题.

5. Baselines in Policy Gradients--降低方差

EGLP lemma说明任何只依赖状态的函数$b$的期望log梯度为0

(-1)

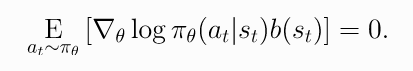
因此在公式里减去一个baselines不影响最后的梯度. 所以有了加入baseline的trick.

(10)

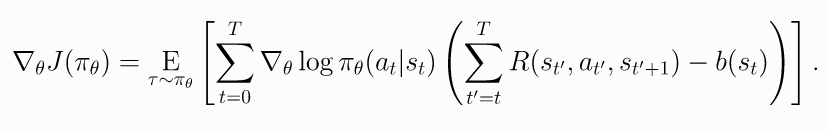
为什么加入baseline? 如果r总是正的, 可以通过log概率调整动作分布. 但是因为是sampling, 有些动作没有抽样到, 其概率分布会变小. 一般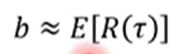

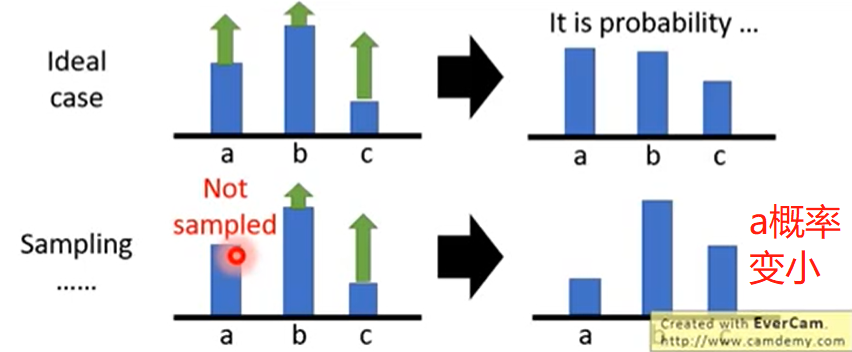
动作a因为没被抽样到, 概率会变小, 但a可能是个好动作

常用的baseline是 on-policy value function $V^{\pi}(s_t)$. 该值是从状态s出发根据策略$\pi$行动的平均回报.

一般选择$b(s_t) = V^{\pi}(s_t)$可以在sample估计中减策略梯度的方差, 加速训练. 一般使用的值函数用神经网络近似, 使用MSE训练,

(-1)

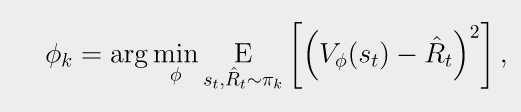
6. 策略梯度其他形式

目前策略梯度的通用形式为

(11)

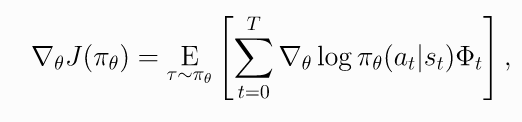
其中$\Phi$可以有多种形式

(11.1)

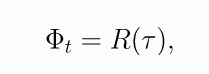
(11.2)

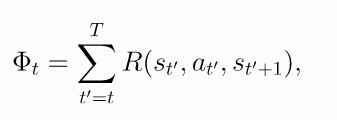
(11.3)

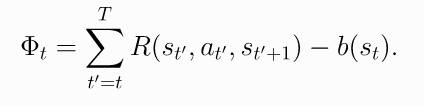
(11.4)

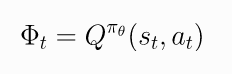
1. The Advantage Function. 优势函数定义为

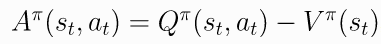
(11.5)

,

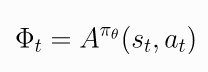重要论文: 广义优势估计( Generalized Advantage Estimation, GAE)