1 百面ML-3降维/非监督学习
1. 降维
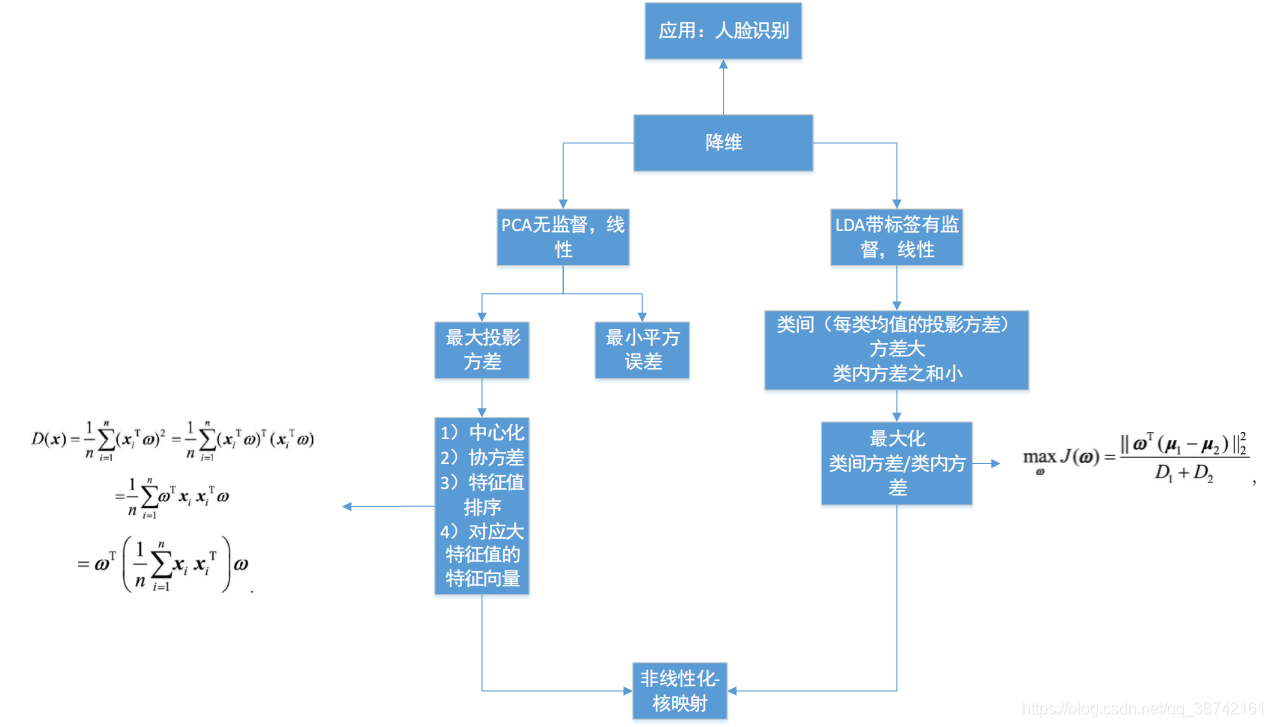
1.1 主成分分析
- 最大化投影方差:
- 方向: 对样本数据进行中心化之后, 对协方差矩阵做特征分解, 最大特征值对应的特征向量
- 最小化均方误差
- 找一个d维超平面, 使得所有点到其距离的平方和最小
SVD分解方法
- 对矩阵A进行中心化之后进行SVD分解与PCA等价
- SVD由迭代求解方法, 直接对矩阵进行特征分解复杂度很高.

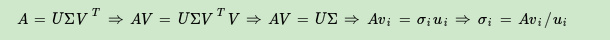
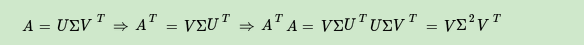


1.2 线性判别分析 LDA
具体步骤:
- 计算每个类别的均值向量和总体均值向量;
- 计算类内散度、全局散度、并相减得到类间散度;
- 对上述最大化目标进行特征分解,并从大到小排列;
- 选取前d个。
2 无监督学习
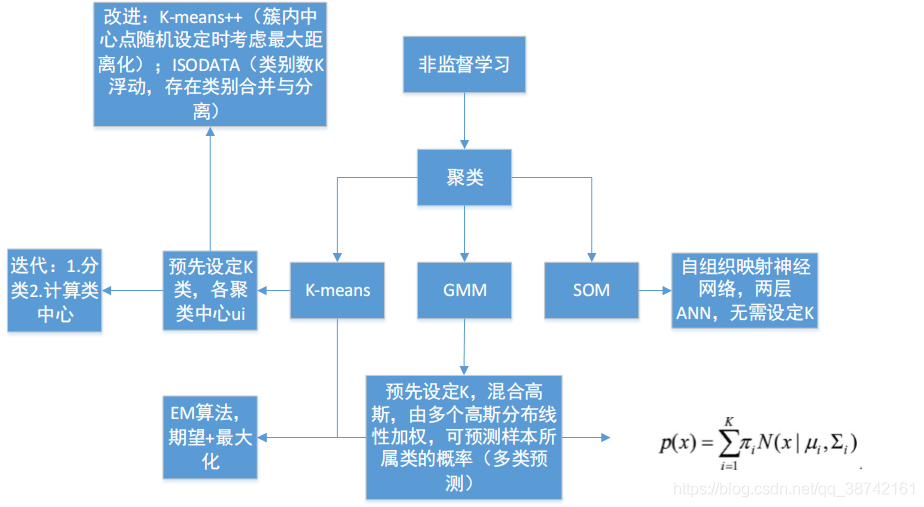
2.1 K-means
简述K均值算法的具体步骤(2)
- 数据预处理, 如归一化, 离群点处理等
- 随机选择K个簇中心
- 定义代价函数: J=所有样本到其所分类别的距离平方和最小
- 迭代如下过程知道代价函数J收敛.
- 对每一个样本, 分配到距离最近的簇;
- 对每一个簇K, 重新计算该簇的中心
优点:
- 对于大数据集, K均值聚类算法相对是可伸缩和高效的,
- 计算复杂度是O(NKt)接近于线性
- 尽管算法是以局部最优结束, 但是一般情况下达到局部最优已经可以满足聚类的需求.
缺点:
- 受初值和离群点的影响每次的结果不稳定,
- 通常不是全局最优而是局部最优解,
- 无法很好的地解决数据簇分布差别较大的情况(比如一类是另一类样本数量的100倍)
算法调优:
- 数据归一化和离群点处理
- 合理选择K值: 手肘法