4 周博磊RL-6-策略优化

优势:
- 收敛性好, 至少是局部最优;
- 在高维动作空间更高效, PG输出是向量, value-based只是单值;
- 可以学习随机策略, value-based不可以. 比如剪刀石头布游戏, 随机更好.
劣势
- 经常收敛到局部最优;
- 评估策略方差比较大.

1. 策略梯度

推导
对于无法求导的性能函数,可以使用Cross Entropy Method (CEM)或者有限微分(Finite Difference)

score-function, $\triangledown_\theta \log \pi_\theta(s,a)$ score function指的应该是每个样本会对应一个score, 这个score近似衡量了这个样本对于log likelihood的贡献. 最终的log likellihood就是每个样本的score加起来再加上一个常数. 因此, 当score的方差大的时候, 每个样本就提供了关于loglikelihood更多的信息, 所以用MLE估计参数的时候, 得到的参数估计的方差反而越小.

(1)

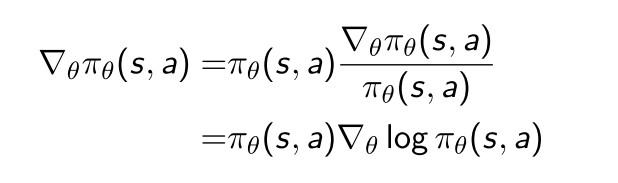
策略举例

考虑离散和连续, 使用softmax和高斯, 其导数如下

2 策略函数优化

spinup-PG

A2C

参考链接

3 PG 改进

PG问题:

on-policy样本效率低, 用同一policy进行串行地采样和优化, 采样效率低;
训练不稳定. 数据相关性大, (策略出错->错的样本->更坏的策略)导致训练崩溃, 无法自动修正偏差.

优化方向:

样本效率低: 重要性采样(TRPO)
不稳定: 限制策略更新的置信区间. (natural PG, TRPO)

3.1 重要性采样公式

(2)

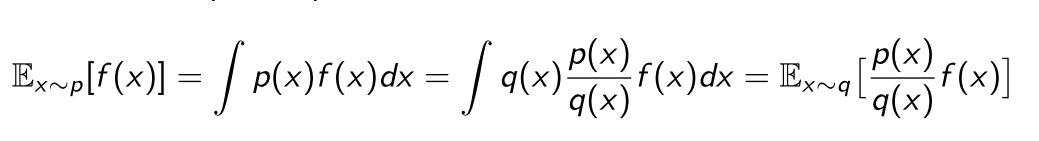
(3)

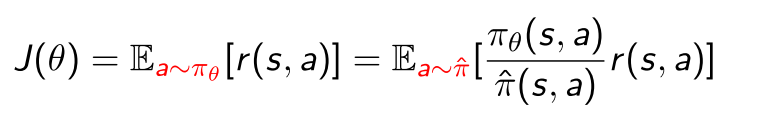
3.2 Natural Policy Gradient

纯PG算法再参数空间进行梯度上升, ==这种方法只考虑了更新最快的方向, 没有和策略联系起来, 而且对参数地初始化非常敏感==.

因此, 可以考虑在分布空间(策略输出)上进心梯度上升, 即加入KL散度作为约束项, 控制分布空间的更新速度, 而不管曲率, (因为只关心由参数诱导的分布的, 因此更鲁棒.)

(1)

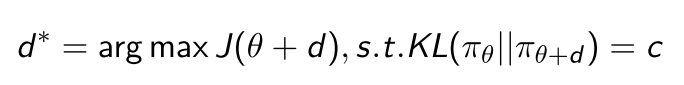
由此将问题转化为带约束最优化问题

增加置信区间的鲁棒性

(4)

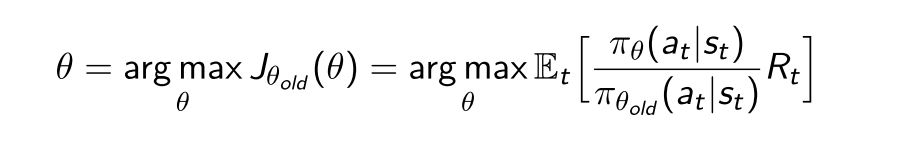
但是比率太大会导致训练不稳定性, 步长太大容易跳过最优解, 所以要限制这个比例的大小, 所以引入一个限制, 用KL散度:

(5)

NPG推导之后的形式:

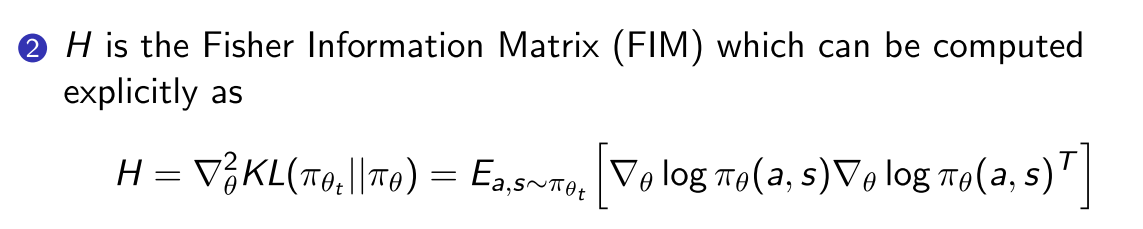
好处:

不用显示设置学习率, 只用设置一个置信区间的大小 $\delta$ .
参数的剧烈变化不会显著改变策略网络的输出.

伪代码

3.3 TRPO

NPG+important sampling的改进版.
近似计算Fisher Information Matrix (FIM)的方法, 通过解线性方程 $Hx=g$ 的方法估计 $x=H^{-1}g$

TRPO伪代码
TRPO 论文证明了, 在迭代的过程中, 每一步都能产生更好的策略, 即通过在每步迭代中最大化 $M_t$ , 可以保证真实目标函数 $J$ 不下降:
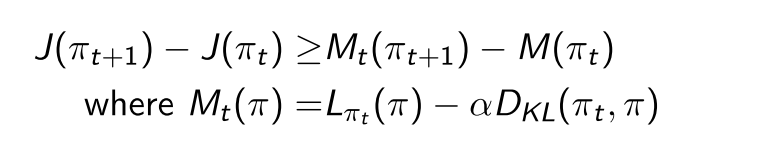
TRPO算法是MM算法的一个实例,
- 目标函数最小化问题: 此时MM表示Majorize-Minimization, 每次迭代找到原非凸目标函数的一个上界函数, 求上界函数的最小值.
- 目标函数最大化问题: 此时MM表示Minorize-Maximization, 每次迭代找到原非凸目标函数的一个下界函数, 求下界函数的最大值.
- 期望最大化(EM)算法可以被视为MM算法的特殊情况, 在EM算法中通常涉及条件期望, 而在MM算法中, 凸性和不等式是主要焦点.
TRPO的问题
- 为当前策略求 $H$ 计算量大, 二阶优化
- 逼近H需要large batch of rollouts
- 共轭梯度(CG)算法实现复杂

3.4 ACKTR

思想来源:
- SGD是一阶优化方法, 优化效率低
- Natural Gradient Descend可以通过二阶优化加速收敛, 但是需要有H矩阵求逆过程
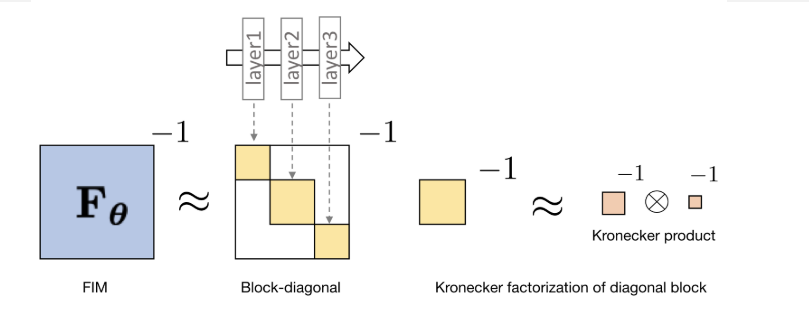
通过Kronecker-factored Approximate Curvature (K-FAC)加速H矩阵求逆运算.

3.5 PPO

spinningup PPO

4. 值函数主线

Q-learning
DDPG
TD3
SAC

4.1 DDPG

对初始化很敏感

4.2 TD3

只能用于连续动作空间.

主要解决Q值过估计的问题.

Clipped Double-Q Learning.
- double Q function
- 每个Q函数都有一个target net, 用估值小的target输出计算TD Target.
- $y(r, s', d) = r+\gamma(1-d)min_{\color{red}{i=1, 2}}Q_{\phi_{i, targ}}(s', {\color{red}{a_{TD3}(s')}})$
Target Policy Smoothing.往target action中加入噪声并clip,
- ${\color{red}{a_{TD3}(s')}} = clip(\mu_{\theta, targ}(s')+clip(\epsilon, -c, c), a_{low}, a_{high} ), \epsilon\sim \mathcal{N}(0, \sigma)$
- $\epsilon$ 加入噪声
- clip起到正则化作用, 避免策略出现尖峰.
“Delayed” Policy Updates. TD3策略网络的更新比Q网络更新慢. paper建议每两次Q更新一次policy.
代码: https://github.com/sfujim/TD3/

4.3 SAC

基础版本只能用于连续动作空间, 但是可以改进成离散动作空间.

使用off-policy优化随机策略, 通过加入熵正则化项, 把随机策略优化和DDPG方法结合.

Entropy-regularized RL:策略优化目标为最大化预期回报和熵(策略的随机性)之间的权衡

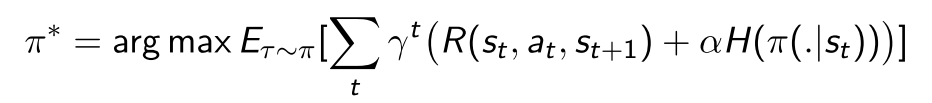
熵正则化项本质为了保证探索性

与TD3一样, 也使用了double Q函数, 计算目标时也是用较小的target Q;

策略优化: 使用Reparameterization trick. 可以把关于动作的期望写成关于噪声的期望.
- 因为动作分布取决于策略参数, 会造成样本和参数的相关性.
- 使用Reparameterization之后, 动作分布就与策略参数去相关了

Reparameterization技术介绍
- 假设要求如下期望: ${\color{red}{\triangledown_\theta E_{x\sim p_\theta(x)}[f(x)]} }$ , x采样值严重依赖于参数 $\theta$ 的分布
- 可以通过引入一个与 $\theta$ 独立的噪声变量 $\epsilon$ 重写采样函数;
- 将x重参数化为 $\epsilon$ 的函数, $p_\theta$ 的随机性被 $q(\epsilon)$ 代替, 则 $g_\theta(\epsilon)=\mu_\theta+\epsilon \sigma_\theta, where \epsilon \sim \mathcal{N}(0, 1)$

代码: https://github.com/pranz24/pytorch-soft-actor-critic/blob/master/sac.py

4 周博磊 RL-56-策略优化