4 周博磊RL-5-值函数逼近

1 TD与MC

1. MC
   • G是无偏的, 但是是对真实V值进行noisy采样, 所以方差大;
   • $E[G_t] =v(s_t)$
   • 线性: $\Delta w=\alpha(G_t-\hat{v}(s_t, w))\triangledown_w \hat{v}(s_t, w) =\alpha(G_t-\hat{v}(s_t, w))x(s_t)$
2. TD
   • TD target $R_{t+1}+\gamma \hat{v}(s_{t+1}, w)$是真实V的有偏采样.
   • $R_{t+1}+\gamma \hat{v}(s_{t+1}, w) \neq v(s_t)$
   • 线性: $\Delta w=\alpha(R+\gamma \hat{v}(s', w)-\hat{v}(s, w))\triangledown_w \hat{v}(s, w) =\alpha(R+\gamma \hat{v}(s', w)-\hat{v}(s, w))x(s)$

2 基础

3 TD近似的收敛性问题

TD在off-policy和非线性近似的时候为什么不稳定?

以下问题引入了太多误差累积/

1. sarsa或者Q-learning在计算的时候,梯度里也包含了用当前参数计算下一步状态值;
2. 同时, 更新过程中设计两个近似过程:
   • 用梯度更新近似bellman方程迭代
   • 对价值函数的近似
3. 在off-policy的时候, 行为策略和目标策略不同, 导致值函数估计不准确

死亡三角

1. 函数逼近. 近似引入误差.
2. bootstrapping. 比如TD,也是引入噪声; 而MC方法相对好,因为是无偏的,不用bootstrapping.
3. off-policy. 行为策略和目标策略不同, 可能导致miss online ,也是引入不确定因素

DQN及其改进

算法

DQN 算法

实现和demo

1 Demo of Breakout by DQN 2 Demo of Flappy Bird by DQN 3 Code of DQN in PyTorch 4 Code of Flappy Bird

改进

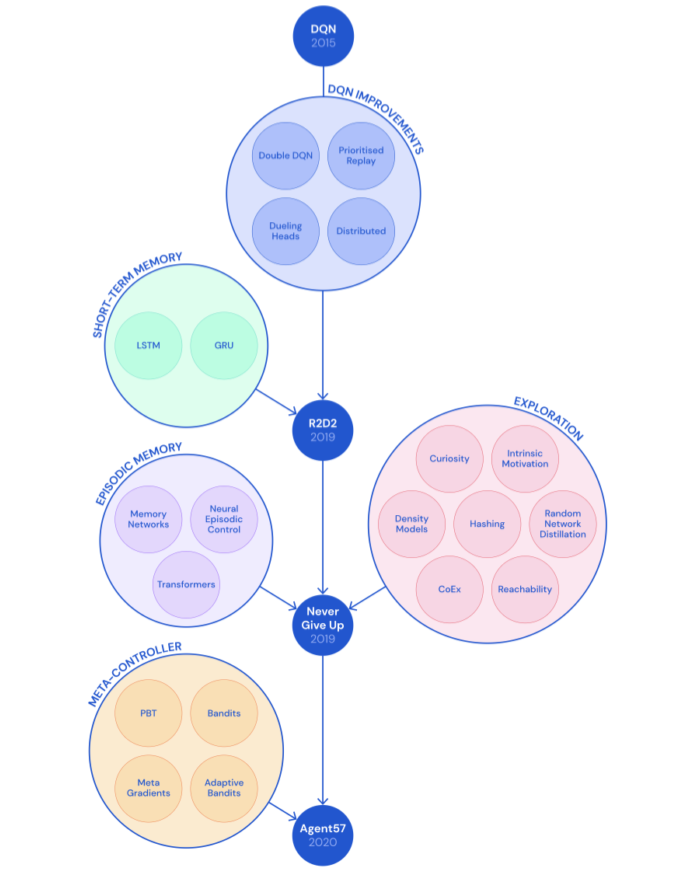
Agent57

代码示例

作业1

https://github.com/cuhkrlcourse/RLexample/blob/master/modelfree/q_learning_mountaincar.py

tutorial on the relevant algorithms