1 百面 ML-3 经典算法

1 LR 算法

1.1 原理

基本原理

1. 通过 sigmoid 函数将样本 x 预测值映射到(0, 1)之间, 并且在做分类任务时, 将$e^{wx+b}/1+e^{wx+b}$作为分类为 1 的概率, $1/1+e^{wx+b}$作为分类为负样本的概率.

2. LR 模型的基本假设还是 模型输出 Y=1 的对数几率时关于 x 的线性函数. 即

   $log \frac{P(Y=1|x)}{1-P(Y=1|x)}=w \cdot x$

训练

在训练时, LR 的 loss 可以使用极大似然估计

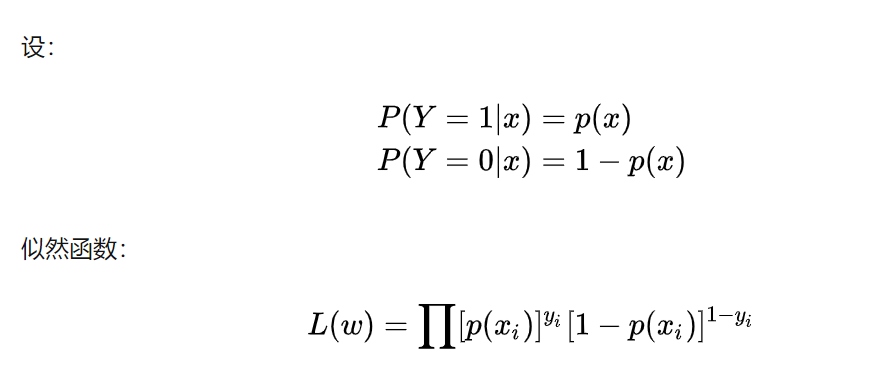
为了更方便求解, 我们对等式两边同取对数, 写成对数似然函数:

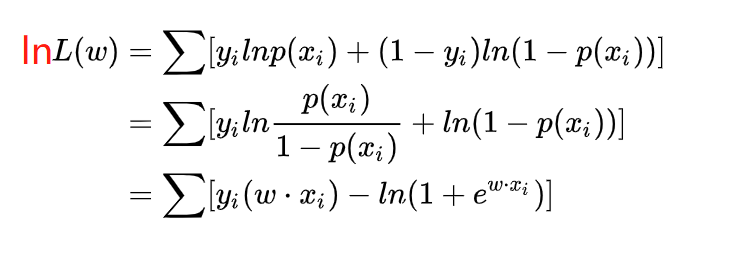
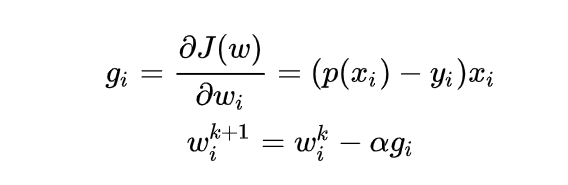
牛顿法

牛顿法的基本思路是, 在现有极小点估计值的附近对 f(x) 做二阶泰勒展开, 进而找到极小点的下一个估计值. 假设 $w^k$ 为当前的极小值估计值, 那么有:

1.2 线性回归和逻辑回归的异同

1. 线性回归做回归，LR 是分类任务；
2. LR 可以不符合线性关系.
3. 逻辑回归因变量是离散的，线性回归因变量是连续的。
4. 两者都用极大似然估计建模，也都可以用梯度下降方法求解。

1.3 优缺点

1. 优点
   • 实现简单, 计算代价不高, 易于理解和实现, 广泛的应用于工业问题上;
   • 分类时计算量非常小, 速度很快, 存储资源低;
   • 便利的观测样本概率分数;
   • 对逻辑回归而言, 多重共线性并不是问题, 它可以结合 L2 正则化来解决该问题;
2. 缺点
   • 当特征空间很大时, 逻辑回归的性能不是很好;
   • 容易欠拟合, 一般准确度不太高
   • 不能很好地处理大量多类特征或变量;
   • 只能处理两分类问题(在此基础上衍生出来的 softmax 可以用于多分类), 且必须线性可分;
   • 对于非线性特征, 需要进行转换;

2 决策树

特征选择, 树的构造, 树的剪枝

2.1 ID3：最大信息增益(互信息)， 熵-条件熵, g(D,A)=H(D)-H(D|A)

• 倾向于选取值多的特征
• 只能处理离散变量, 只能用于分类, 对缺失值敏感, 可多分支

2.2. C4.5：最大信息增益比

• 对 ID3 进行了优化, 平衡了分类的问题, 对取值比较多的特征进行了惩罚, 在 ID3 基础上除以关于特征的熵.
• $g_R (D,A)=\frac{g (D,A)}{H_A (D)}, H_A (D) = - \sum_{i=1}^{n}\frac{|D_i|}{|D|} \log _2 \frac{|D_i|}{|D|}$, n 是特征个数.
• 可以处理连续变量, 进行切分, 只能用于分类, 可多分支

2.3. CART：只能二分类(基尼系数最小化), 可回归(MSE 损失最小化)

• $Gini(p)=\sum_{k=1}^K p_k(1-p_k)=1-\sum_{k=1}^K p_k^2$
• 二分类: $Gini(p)=2p(1-p)$
• 二元树, 当基尼指数降为 0, 完成决策树的生长.

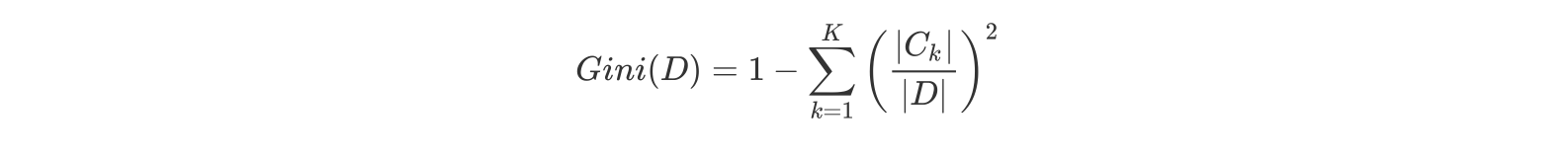
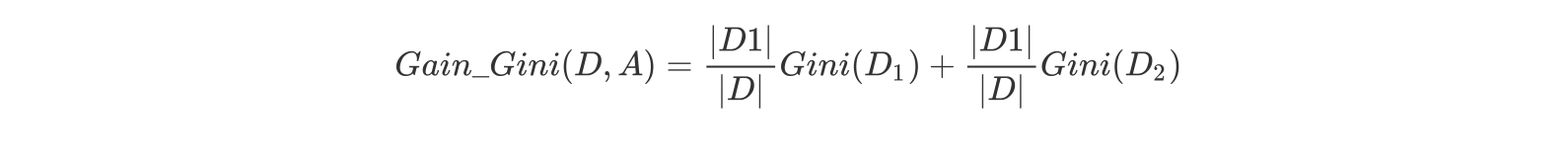
对于属性 A，分别计算任意属性值将数据集划分为两部分之后的 Gain_Gini，选取其中的最小值，作为属性 A 得到的最优二分方案。 然后对于训练集 S，计算所有属性的最优二分方案，选取其中的最小值，作为样本及 S 的最优二分方案。