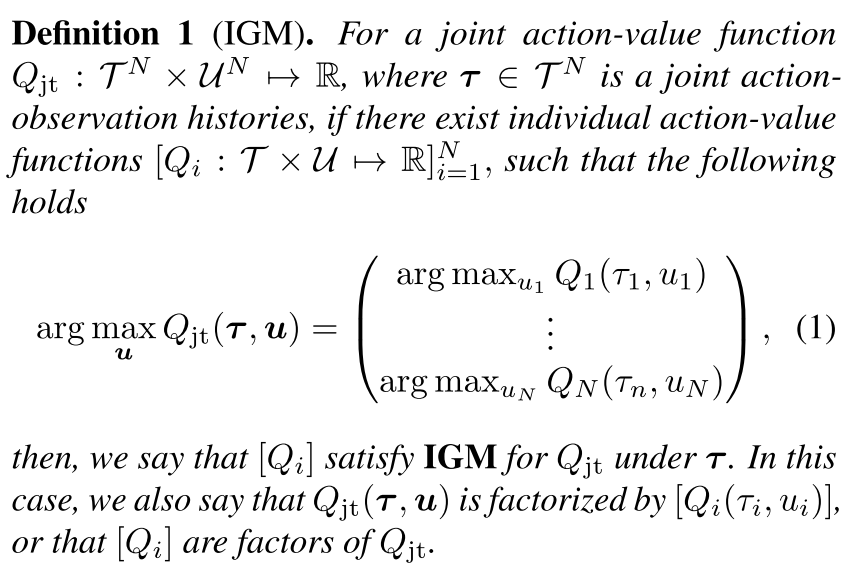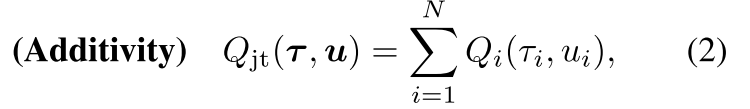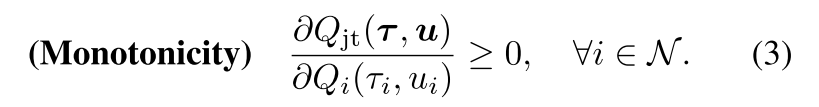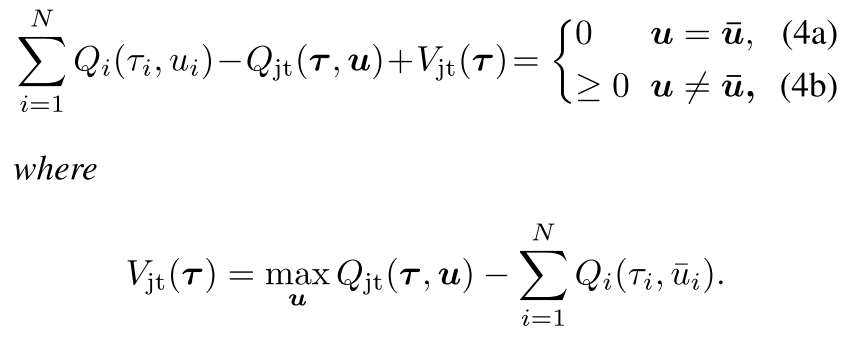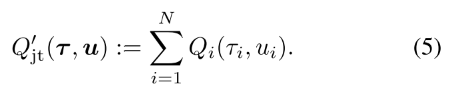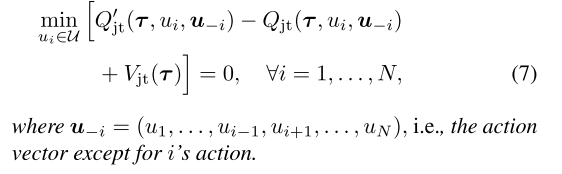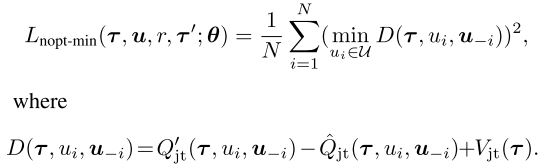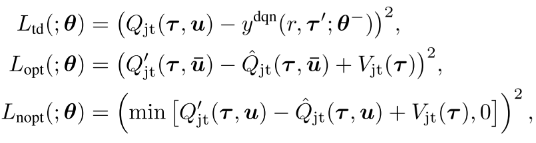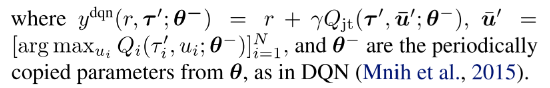4 QTRAN

QTRAN: 基于Transformation机制的协作多智能体强化学习值分解方法

论文:Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement learning

1 概述

定义: IGM (Individual-Global-Max)

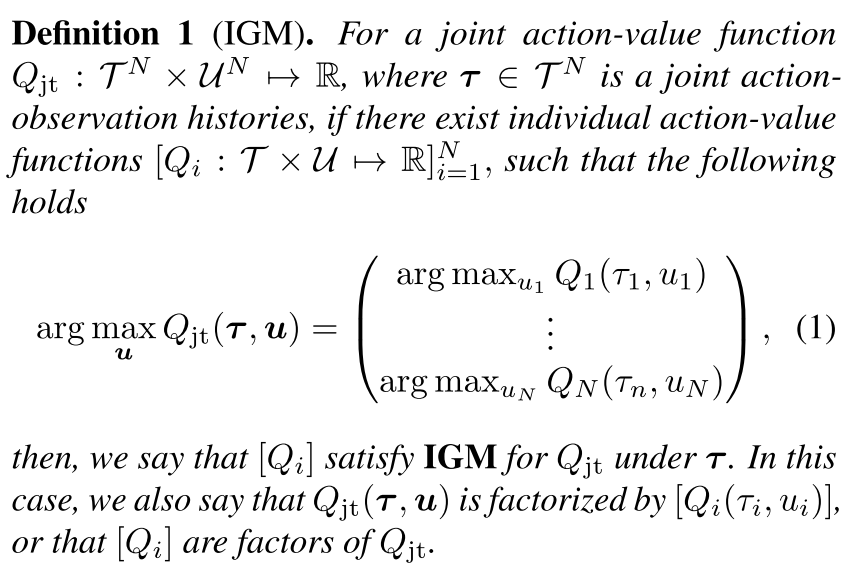
算法演变:

• 去中心化方法, 可扩展性好, 但是存在不稳定问题;
• 中心化方法: 可以解决非稳定问题, 但是随智能体增加, 复杂性爆炸;
• MADDPG: 学习在连续动作空间的分布式策略;
• COMA: Actors用联合critic估计反事实baseline解决信用(贡献)分配问题;
• 值分解方法: 解决联合Q值随着智能体数量增加, 复杂性爆炸增加的问题,
  • VDN: 加性约束,
  • 
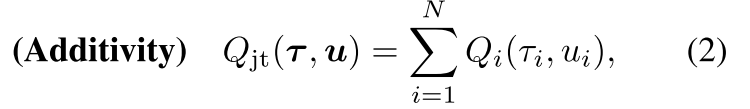
  • QMIX: 单调性约束.
  • 

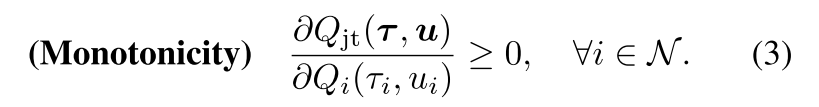
本文目标:

可分解任务定义为, 联合Q值取得最优动作也是个体Q值得最优动作. 使用加性限制和单调性限制有点过度限制了, 限制了智能体的种类;

本文把原始联合Q值函数$Q_{jt}$转换为新的$Q_{jt}'$, 使其与$Q_{jt}$具有相同的最优动作, 并解除加性/单调性约束.

本文贡献:

• 通过学习一个状态值函数(用来更正部分观察带来得偏差), 把原始联合动作值函数转化为新的易分解形式, 且最优动作保持相同;
• QTRAN算法: 联合动作值网络、个体动作值网络、状态网络, 定义每个网络的loss函数;
• QTRAN变体: QTRAN-base和QTRAN-alt
  • 不同点: 如何构造非最优动作的转换Q函数
  • 收敛速度和稳定性
• 在三个环境测试算法.

2 算法原理

2.1 因子函数$[Q_i]$的充分条件

定义$\bar{\mu}_i=argmax_{\mu_i}Q_i(\tau_i, \mu_i)$表示最优动作, $\bar{\mathbf{u}}=[\bar{\mu}_i]_{i=1}^{N}$; 令$\mathbf{Q}=[Q_i]\in \mathbb{R}^N$, 即$Q_i, i = 1, ..., N$的列向量.

定理1 给出$[Q_i]$满足IGM的条件.

一个可分的联合Q值函数$Q_{jt}(\mathbf{t}, \mathbf{u})$, 可以被$[Q_i(\tau_i, \mu_i)]$分解, 当

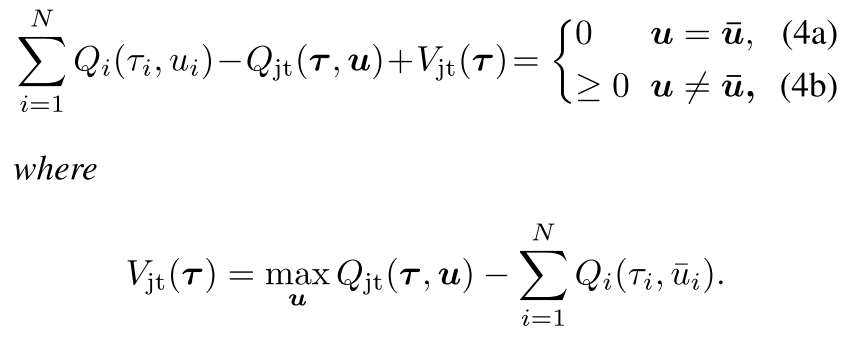注意, (4)中的条件在仿射变换的情况下是必要的. 也就是说, 存在一个仿射变换$\phi(\mathbf{Q}) = A\cdot \mathbf{Q}+B$(其中$A=[a_{ii}] \in \mathbb{R}_+^{N\times N}$是$a_{ii}>0$的对称对角矩阵, $B=[b_i]\in \mathbb{R}^N$), 使得当$Q_{jt}$可以被$[Q_i]$分解时, 把$Q_i$替换成$a_{ii}Q_i+b_i$时, 则(4)成立. 这是因为对于所有的i, $b_i$都抵消掉, $a_{ii}$仅仅作为$\sum_{i=1}^N Q_i$的缩放因子, 因为IGM是不变的.

变换分解:首先定义加性的变换联合Q值函数,

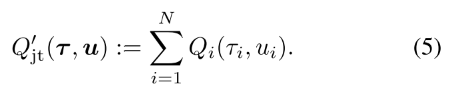
通过加性结构, $[Q_i]$满足$Q'_{jt}$ 的IGM, 那么它就是$Q'_{jt}$的分解个体Q值函数. 因为$argmax_{\mathbf{u}}Q_{jt}(\mathbf{t}, \mathbf{u})= argmax_{\mathbf{u}}Q'_{jt}(\mathbf{t}, \mathbf{u})$, 找到$[Q_i]$满足(4)就是$Q'_{jt}(\mathbf{t}, \mathbf{u})$的分解.

函数$V_{jt}(\mathbf{t})$用来修正中心化联合Q函数$Q_{jt}$和$[Q_i]$的和的偏差. 偏差是智能体部分观察带来的. 如果加入了全局观察, $V_{jt}$可以设为0.

2.2 算法

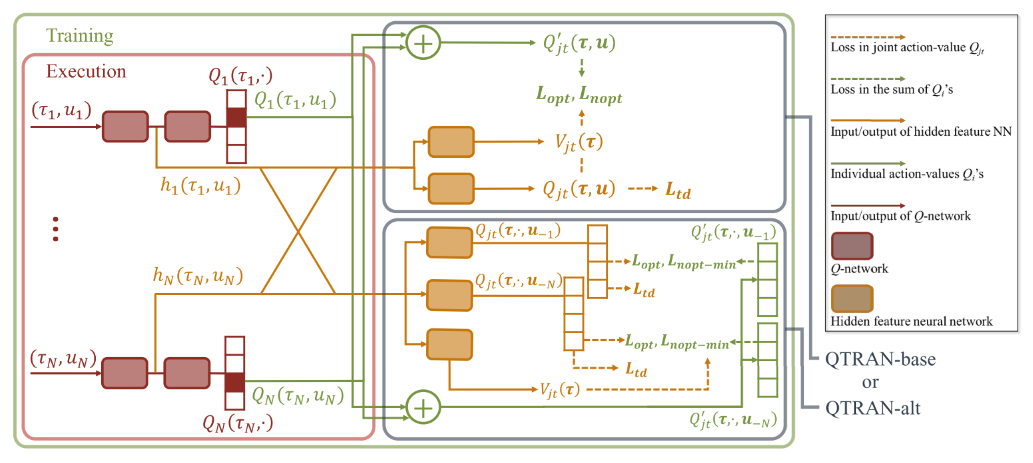Figure 1. QTRAN-base and QTRAN-alt Architecture

QTRAN包含三个独立的估计器: 每个智能体i的独立Q值网络, 联合Q值网络(可以分解为$Q_i$), 状态价值网络

在Individual action-value network中, 每个智能体i的Q值加和得$Q'_{jt}$;

联合Q网络: 逼近$Q_{jt}$, 输入为选择的动作, 输出为该动作得Q值.

• 首先使用所有个体Q网络采样的动作向量来更新联合Q网络. 因为联合动作空间$\mathcal{U}^N$, 找到最优联合动作复杂度很高, 而每个个体的最优动作取argmax就行, 是线性的.
• 第二, 联合Q网络共享个体网络低层的参数, 联合Q网络把个体网络隐层特征加和整合$\sum_i h_{Q, i}(\tau_i, u_i)$, 其来自于$h_i(\tau_i, u_i)=[h_{Q, i}(\tau_i, u_i), h_{V, i}(\tau_i)]$.(使用此参数共享样本效率高, 可进行可扩展的训练, 但会牺牲表达能力.)

状态值网络: 计算标量状态价值, 类似与dueling网络的$V(s)$.

• 用来在计算argmax时匹配$Q_{jt}$和$Q'_{jt}+V_{jt}$. 没有V, 部分观察可能限制$Q'_{jt}$的表达复杂性;
• 给定$\mathbf{t}$, 状态值独立于选择的动作, 因此对动作选择没有贡献, 所以使用公式(4)代替.
• 输入也是个体网络隐特征的组合$\sum_i h_{V, i}(\tau_i)$

2.3 损失函数 QTRAN-base

目标:

• 训练联合Q值$Q_{jt}$估计真实动作值;
• 变体值函数$Q'_{jt}$应该追踪到联合Q值$Q_{jt}$, 使其最优值相等.
• 使用目标网络和replay buffer

其中

• $r$是在观察$\tau$执行动作$u$转移到$\tau '$的奖励.
• $L_{td}$学习$Q_{jt}$, 通过最小化TD误差估计真实Q值;
• $L_{opt}$和$L_{nopt}$为了在把$Q_{jt}$分解为$[Q_i]$时满足条件(4).
• $L_{nopt}$用来在每一步检查样例中选择的动作是否满足(4b), $L_{opt}$检查最优局部动作是否满足(4a).
• 根据网络对样本中动作满足(4a)或(4b)的程度定义损失, 实现(4); 但是验证(4a)需要太多样本, 因为最优动作很少, 需要大量采样.
• 因为目标是学习$Q'_{jt}$和$V_{jt}$分解给定的$Q_{jt}$, 本文在学习$L_{opt}$和$L_{nopt}$时通过固定$Q_{jt}$稳定学习.
  • 
  • 

2.4 QTRAN-alt

使用一种反事实方法, 前述定理1通过(4a)强化IGM, 通过(4b)确定个体Q值$[Q_i]$和状态值$V_{jt}$如何跟踪$Q_{jt}$, 控制构造函数的稳定性.(4b)过于稀疏导致不能构造正确的分解形式, 也就是说, (4b)对于非最优动作施加了坏的影响, 反过来影响稳定性和收敛速度. 关键在于如何在非最优动作处应强化什么条件.

定理2

定理1及其必要条件通过替换(4b)为(7)成立:

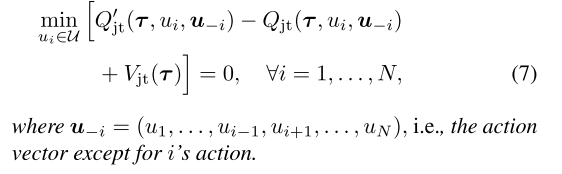条件(7)在遵循定理1的同时令至少一个动作为0, 条件比(4b)更强.(4b)要求对任意$\tau$, $Q_{jt}(\mathbf{t, u})-V_{jt}(\mathbf{t}) \le Q'_{jt}(\mathbf{t, u}) \le Q'_{jt}(\mathbf{t}, \bar{\mathbf{u}})$, 此时可能存在$Q'_{jt}(\mathbf{t}, {\mathbf{u}})$和$Q'_{jt}(\mathbf{t}, \bar{\mathbf{u}})$相近, 但是$Q_{jt}(\mathbf{t, u})$比$Q_{jt}(\mathbf{t}, \mathbf{\bar{u}})$小很多. 带来不稳定.

条件(7)限制了上述问题, 加宽了$Q_{jt}(\mathbf{t, u})$和$Q_{jt}(\mathbf{t}, \mathbf{\bar{u}})$之间的gap.

QTRAN-alt网络只用一次前向, 就可以计算所有i的$Q_{jt}(\mathbf{t, \cdot}, \mathbf{u}_{-i})$和$Q'_{jt}(\mathbf{t, \cdot}, \mathbf{u}_{-i})$.

因此, 每个智能体都有一个反事实联合网络, 给定其他智能体的动作, 其对于每个可能动作的输出为$Q_{jt}(\mathbf{t, \cdot}, \mathbf{u}_{-i})$. 从其他智能体得到$h_{v, i}(\tau_i)$和合并隐特征$\sum_{j \ne i} h_{Q, j}(\tau_j, u_j)$.

最后, 对于所有智能体, $Q'_{jt}(\mathbf{t}, \cdot, \mathbf{u}_{-i}) = Q_i(\tau_i, \cdot) + \sum_{j \ne i}Q_j(\tau_j, u_j)$. 通过损失函数用$L_{nopt-min}$代替$L_{nopt}$实现:

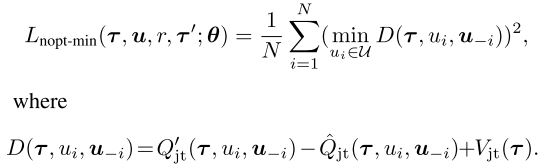
2.5 矩阵游戏说明VDN和QMIX无法达到联合最优

该游戏是合作MARL问题, 且不满足加性或者单调性约束, QTRAN成功学习联合Q值, VDN和QMIX不能.

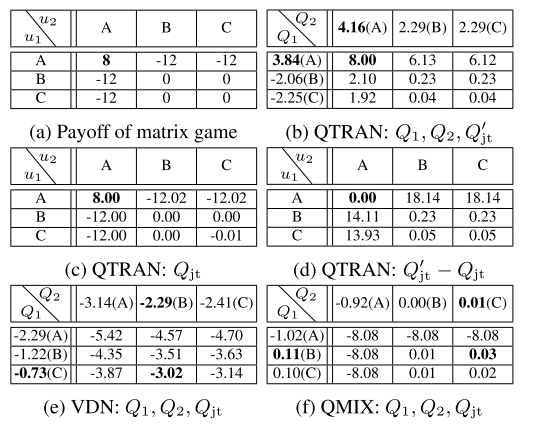表1, 在矩阵游戏中重构联合Q值的结果

在有21个动作的矩阵游戏中测试QTRAN-base和QTRAN-alt.

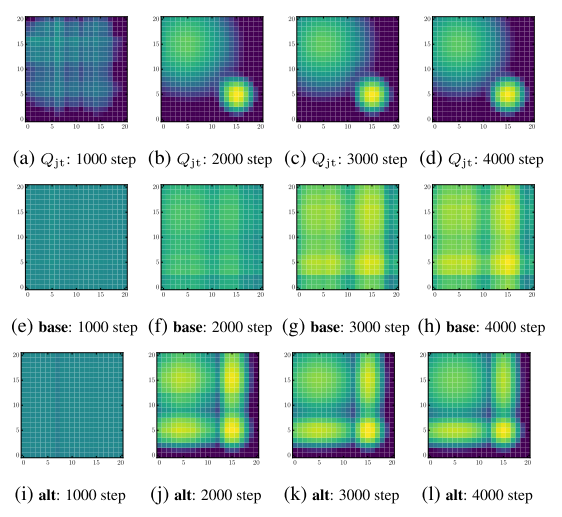图2, (a-d)表示$Q_{jt}$, (e-l)表示$Q'_{jt}$

表明两个算法都学会了最优动作, alt算法在非最优点估计更准确.

3 实验

3.1 多域高斯压缩Multi-domain Gaussian Squeeze (MGS)

GS是简单非线性多智能体资源分配问题, 多个同质智能体分配资源同时避免拥塞. 本文使用MGS:

• 有10个智能体
• 每个智能体i执行动作$u_i$, 控制资源利用等级(0-9); 每个智能体都有自己的单元级的资源数量, $s_i\in [0, 0.2]$, 作为环境先验;
• 联合动作$\mathbf{u}$决定整体资源使用$x(\mathbf{u}=\sum_i s_i\times u_i)$
• 假设有$K$个域需要分配资源, 目标是最大化联合奖励:$G(\mathbf{u}) = \sum_{k=1}^K xe^{-(x-\mu_k)^2 / \sigma_k^2}$, $\mu_k, \sigma_k$是域参数. 单域GS只有一个局部最大值, MGS有多个.
• 另外, MGS有一个新的次优"陷阱"策略, 更容易到达, 但是只有最优回报的一半. 当K>1时用来测试算法很有效.

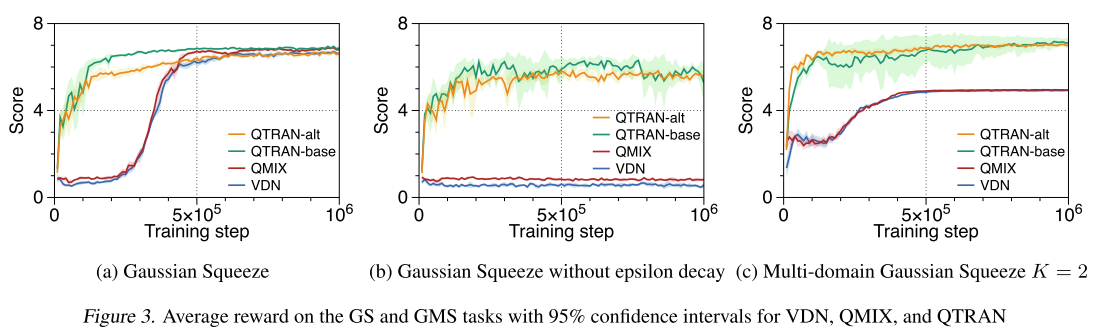
• (a) QTRAN更快, 学习到最优策略. VDN和QMIX的结构性限制, 妨碍学习的准确率, 由于错误的$\epsilon0decay$策略收敛到偏差样本的局部最优点(该点在K=1, 即GS时是全局最优). 为了验证上述假设, 使用完全探索验证.
• (b) QTRAN几乎是相同的策略, 但是VDN和QMIX恶化严重;
• (c) VDN和QMIX学会的是次优策略

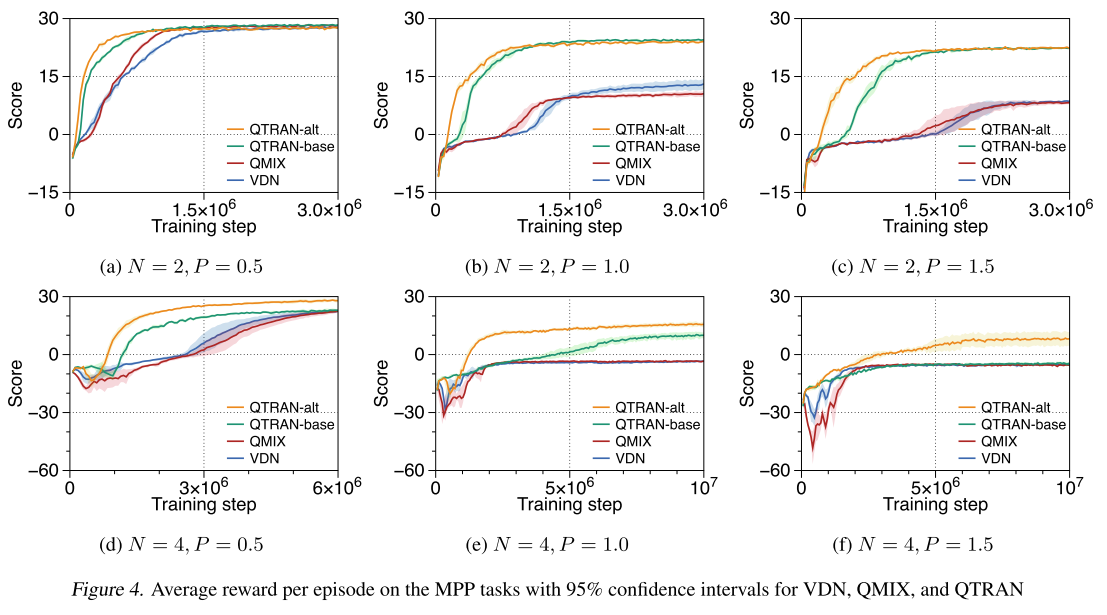
3.2 改进捕食者-猎物游戏Modified predator-prey (MPP)

经典格子游戏, 修改了一些设定:

• 进入视线范围视为捕获, 且只有多个智能体同时捕获猎物才有正向奖励, 要求更高级的合作. 当两个及以上抓住猎物, 奖励1, 当只有一个猎手捕获猎物时, 惩罚-P.
• 注意惩罚P决定了单调程度. P越高, 任务单调性越低
• 猎物随机再生, 游戏固定进行100步, 在6个场景中测试; N=2, 4, P=0.5, 1.0, 1.5; 当N=4时有2个猎物, 否则有1个.

4 附录

4.1 算法伪代码