8-拉格朗日对偶理论

仿射集,仿射函数, 凸集, 凸函数, 凸优化问题相关定义, 可以查看凸优化笔记 0

1. "松弛"与"界"

我们面对数学规划问题中的约束项时, 有时可以很直观地感受到一些约束比较简单, 而另一些约束是比较复杂的.

$\begin{array}{ll} \max & c^{\top} x \\ \text{s.t. } & A x \leq b \quad \text {(nice constraints)} \\ & D x \leq d \quad \text{(complicated constraints)} \\ & x \in X \end{array}$

一个自然而然的想法是能否想办法把这些比较难的约束去掉. 由此引申出优化求解方法中一种重要的思想--"松弛".

关于"松弛", 最容易理解的例子, 莫过于求解线性整数规划问题时, 可以将整数约束转化为整个集合区间上的连续约束, 即"连续松弛". 在得到这样一个线性规划松弛问题之后, 可以使用单纯形或内点法等进行快速求解. 之后使用"分支定(上/下)界"的方法, 使用类似于树搜索的方法求解原问题的最优解.

此外, 还可以将困难的约束直接放进目标函数里, 通过引入一个 price, 对违反该约束的函数取值增加一些代价. 这就是"拉格朗日松弛"的基本思想.

拉格朗日松弛可以比连续松弛提供更紧的界

1.1 示例 1

我们首先看这样一个问题,

$\begin{array}{ll} \min _{x, y} &c^{T} x+d^{T} y \\ \text{s.t. } &A_{1} x=b_{1} \quad (A1)\\ &A_{2} y=b_{2} \quad (A2) \\ &A_{3} x+A_{4} y=b_{3} \quad (A3)\\ & x,y \in D. \end{array}$

很明显, 约束 A1 和 A2 分别只和 x/y 有关, 而约束 A3 把两类变量耦合在了一起。我们看看如果将 A3 放入目标函数, 问题会转为什么样子:

$\begin{array}{ll} \min _{x, y} &c^{T} x+d^{T} y+\lambda^{T}\left(A_{3} x+A_{4} y-b_{3}\right) \\ \text{s.t.} &A_{1} x=b_{1} \\ &A_{2} y=b_{2} \\ & x,y \in D. \end{array}$

这其实相当于分别求如下两个优化问题, 再进行求和:

• 子问题 1

$\begin{array}{ll} \min _{x} & c^{T} x+\lambda^{T} A_{3} x \\ \text{s.t.} & A_{1} x=b_{1} \\ \end{array}$

• 子问题 2

$\begin{array}{ll} \min _{y} & d^{T} y+\lambda^{T} A_{4} y \\ \text{s.t.} & A_{2} y=b_{2} \\ \end{array}$

问题看起来简单了很多. 引入的新变量就是上边所说的 price, 即拉格朗日乘子, 也称"对偶变量".

• price 的意思是, 对于违反松弛的约束的变量取值的情况, 可以通过这个$\lambda$进行惩罚.
  • 求极大, 就让松弛项为负, 使目标值比原来变小; 求极小, 让松弛项为正

这个 price 还有另一层意思, 我们通过松弛引入了原问题的一个下界, 之后我们可以通过调整$\lambda$, 让新问题的最优解的取值满足原来的约束.

1.2 示例 2 整数规划问题

传统整数规划求解方法包括割平面法/动态规划/分支定界等

但是再大规模整数规划问题下, 这些方法无法在可接受的时间内求解. 因此一般寻求对原问题进行分解或松弛, 之后再使用割平面或者分支定界, 快速求解小规模问题的方法. 主要方法分为如下三类.

1. Benders decomposition (主要思想是行生成+割平面方法)
2. Dantzig-Wolfe decomposition (主要思想其实就是列生成)
3. Lagrangian decomposition (主要思想是 Lagrangian relaxation)

考虑如下 0-1 整数规划问题, 我们看一下使用了拉格朗日松弛后会发生什么:

$\begin{array}{lll} (0-1 \mathrm{IP}) & \min & c^T x,\\ & \text{s.t. } & Ax\le b, \\ && x\in \{0,1\}^n \\ \end{array}$

将$Ax \le b$进行松弛, 引入拉格朗日乘子$u\in R^m_+$. 为什么此处的$u$取正值, 下一节会进行介绍.

$\begin{aligned} z(u) &=\min \left\{c^{\mathrm{T}} x+u^{\mathrm{T}}(A x-b) \mid x \in\{0,1\}^{n}\right\} \\ &=-u^{\mathrm{T}} b+\min \left\{\left(c+A^{\mathrm{T}} u\right)^{\mathrm{T}} x \mid x \in\{0,1\}^{n}\right\} \\ &=-u^{\mathrm{T}} b+\sum_{i=1}^{n} \min \left\{\left(c+A^{\mathrm{T}} u\right)_{i} x_{i} \mid x_{i} \in\{0,1\}\right\} \\ &=-u^{\mathrm{T}} b+\sum_{i=1}^{n} \min \left\{\left(c+A^{\mathrm{T}} u\right)_{i}, 0\right\} \end{aligned}$

可以看出, 在求解$z(u)$的时候, 只需要遍历一遍向量$(c+A^{\mathrm{T}} u)$的各个分量, 如果大于 0, $x$就取 0; 如果小于 0, $x$就取 1. 可以在$O(n)$时间内求解.

1.3 一般形式的拉格朗日松弛方法

为了更明确地说明拉格朗日乘子在不同情况下的取值, 下面对等式约束和不等式约束进行分别说明, 混合约束的情况下就是把这两种进行组合.

注:

• 我们将原来的问题称为原始(Primal)问题, 用记号 P 表示

1.3.1 等式约束线性规划

$\begin{array}{llc} (\mathrm{P}) & \min & f(x) = c^T x,\\ & \text{s.t. } & Ax = b, \\ && x \ge 0 \\ \end{array}$

由等式约束$b - Ax = 0$, 引入拉格朗日乘子$\lambda \in R^m$, 得到

$\begin{array}{lc} \min & c^T x + \lambda^T (b- Ax),\\ \text{s.t. } & x\ge 0 \\ & \lambda\in R^m \\ \end{array}$

此时我们得到了一个在很简单的约束上的目标函数. 将其进行进一步整理, 并定义函数:

$\begin{array}{ll} d(\lambda) &= \min_{x\ge0} \{ b^T \lambda + (c-A^T \lambda)^T x \} \quad (1.3.1) \\ &= b^T \lambda + \min_{x\ge0} \{(c-A^T \lambda)^T x \} \quad (1.3.2)\\ \end{array}$

考虑式 1.3.2 右边求极小的项:

$\begin{array}{llll} \text{if} & c-A^T \lambda\ge 0, & d= b^T \lambda, & x^* = 0 \\ \text{if} & c-A^T \lambda < 0, & d=-\infty, & x^* = \infty (\text{infty})\\ \end{array}$

显然原始问题转化为一个关于$\lambda$的函数, 称为对偶函数, 记为$d(\lambda)$.

$d(\lambda)=\left\{ \begin{array}{l} b^T \lambda, \text{ if } A^T \lambda \le c \\ -\infty, \text{ otherwise } \end{array} \right.$

另外一个显然的结论是, 引入松弛项后, 定义域变大了, 实际上是引入了一个原始问题的下界.

• 因为$b-Ax=0$在原始问题的可行域上, d 总能取到不大于原始问题的极小值.

1.3.2 不等式约束线性规划

不等式约束与等式约束类似,

$\begin{array}{llc} (\mathrm{P}) & \min & f(x) = c^T x,\\ & \text{s.t. } & Ax \ge b, \\ && x \ge 0 \\ \end{array}$

通过引入一个额外的辅助变量$s\ge0$, 可以使得

$(A,-I)\left(\begin{array}{c} x \\ s \end{array}\right)=b$

得到了等式约束, 再通过如上一节的等式约束问题的求解过程, 可以得到,

$(A,-I)^{T} \lambda \leq\left(\begin{array}{l} c \\ 0 \end{array}\right) \Rightarrow d(\lambda) = \left\{b^T\lambda |A^T \lambda \le c, \lambda \ge 0 \right\}$

最终的松弛问题是一个关于$\lambda$的优化问题. 特别在不等式约束下, 令$\lambda \ge 0$, 有更好的性质 (注意原始问题不等式约束为大于等于号$\ge$).

1.3.3 一般约束问题

考虑如下优化问题:

$\begin{array}{cl} \min _{x} & f_{0}(x) \\ s . t . & f_{i}(x) \leq 0, i=1,2, \ldots, m \\ & h_{j}(x)=0, j=1,2, \ldots, p \end{array}$

将松弛后的问题称为拉格朗日函数

$\begin{array}{l} L(x, \lambda, v)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{j=1}^{p} v_{j} h_{j}(x), \\ \text{where, }x \in R^{n}, \lambda \in R^{m}, v \in R^{p} \end{array}$

新引入的变量(向量) $\lambda, v$称为拉格朗日乘子

在 1.3.1 节我们也粗略给出过一个对偶函数, 并在简单例子上理解了这是原始问题的一个下界. 我们下面给出拉格朗日对偶函数的正式定义:

将拉格朗日函数关于$x$的下确界, 称为拉格朗日对偶函数:

$d(\lambda, v) = inf_{x} L(x, \lambda, v)$

inf 符号表示取下确界。 即一个集合最大的下界.  **考虑一个开区间(0,1)的下确界是什么?**
求解析式可先将 L 看成是关于 x 的函数，而将拉格朗日乘子看作常数，求出 L 的极小值点;
再将该点代入 L ，得到的关于 λ 和 v 的表达式就是对偶函数。

  在回头看一下 1.3.1 所说的对偶函数是否符合这个定义?

对偶函数具有如下两条重要性质：

1. 对偶函数一定是凹函数，其凹性与原目标函数和约束函数凹凸与否无关。

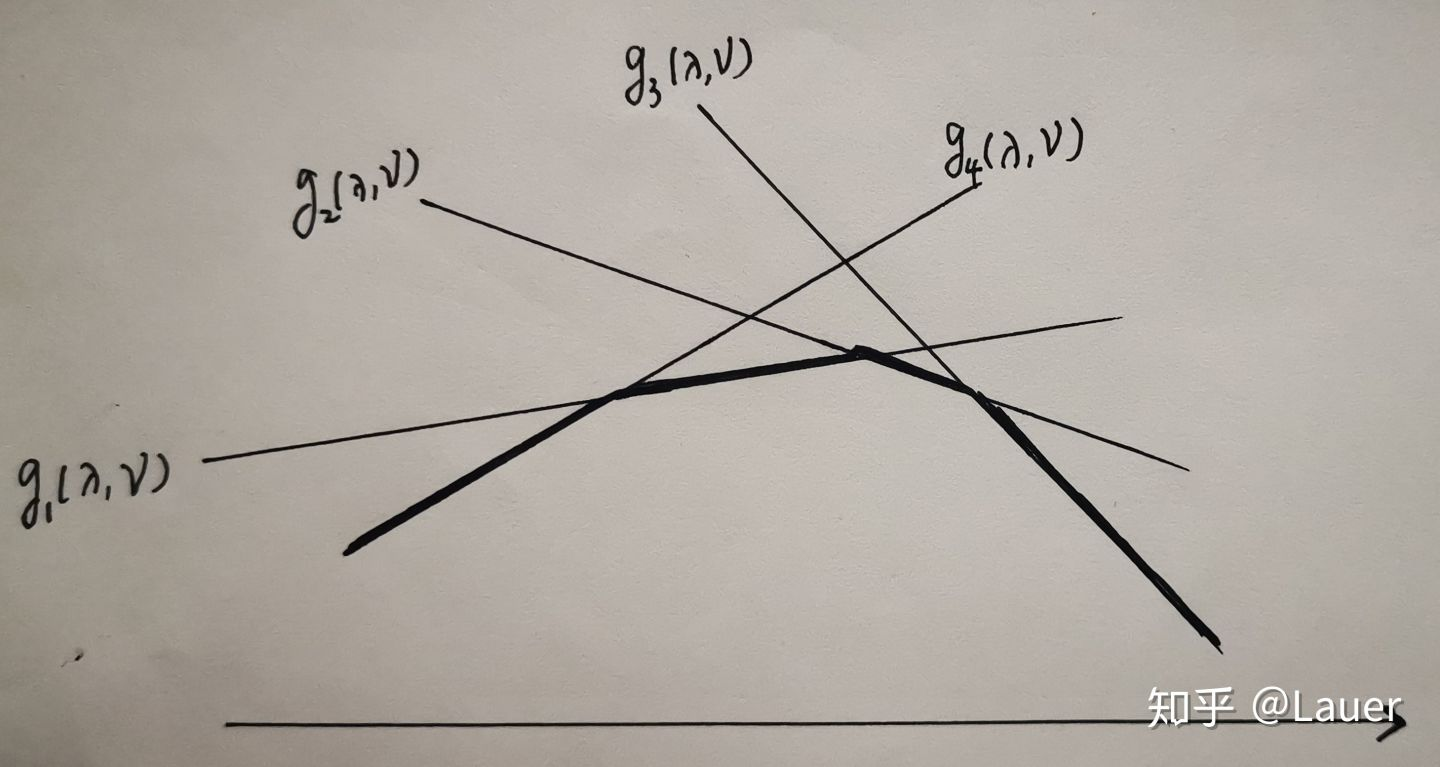
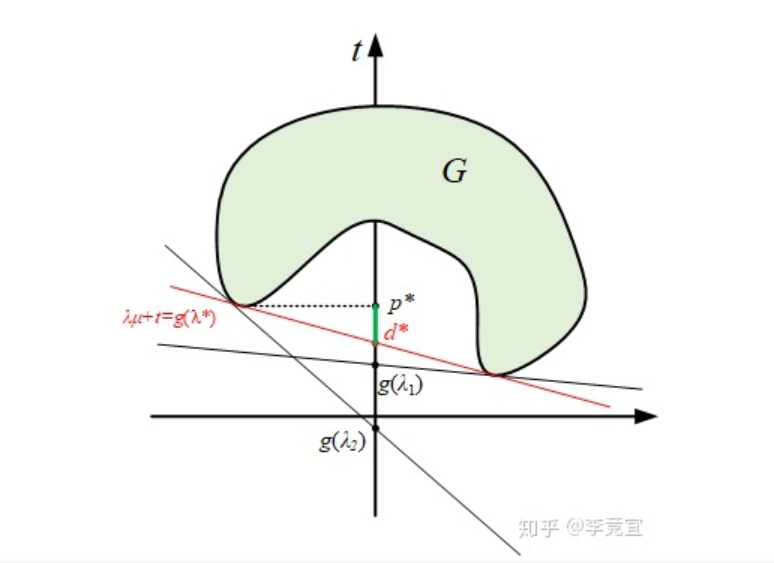
fig 2-3

前边使用不等式线性规划验证了$\lambda$的取值为非负值时, 原松弛问题才是有界的, 下面证明这个界确实是原问题的下界.

2. 对于 ∀ λ ≥ 0, ∀ v（泛指向量中的每个分量），如果原问题最优解对应的目标函数值为p*, 则 g(λ,v)≤p*

关于这个下界和后续对偶的关系,知乎-李竞宜, 给出了更加通俗易懂的解释

以上我们说明了拉格朗日对偶函数得由来, 并证明了其是原始优化问题得下界.

下面可以正式介绍对偶理论.

2 拉格朗日对偶

2.1 拉格朗日对偶问题

根据对偶函数的性质 2 ， 对 $\forall \lambda \geq 0, \forall v$, 对偶函数 $d(\lambda, v)$ 是原问题最优值 $p^{*}$ 的一个下界.

但是, 我们的目的是求原始问题的最优值. 我们废了这么大力气构造了对偶函数有什么意义吗? 其实在数学中我们得到一个下界是很有意义的, 一个最广泛的应用方法是:我们得一个简单的下界函数, 然后通过最大化这个下界函数, 来逼近原问题的最优解.

上图中$d^*$称为对偶间隙 (duality gap). 我们优化的目标其实是最小化这个间隙.

原问题的拉格朗日对偶(Dual)问题, 记为 D, 定义如下:

$\begin{array}{lcl} \text{(D.)} &\quad\max_{\lambda, v} & d(\lambda, v) = min_x L(x, \lambda, v) \\ &\text { s.t. } & \lambda \geq 0 \end{array}$

由于对偶函数是凹函数，故拉格朗日对偶问题一定是凸优化问题，其对应的最优解为 $\lambda^*, v^*$ (最优拉格朗日乘子)，对应的最优值为 $d^*$, 有$d^* \leq p^*$.

2.2 强/弱对偶性

(1) 显然, 针对所有对偶问题, 如果有解, 则$d^* \leq p^*$, 称"弱对偶性"成立.

弱对偶性在有解时存在, 但是并不是我们想要的, 因此我们更希望$d^* = p^*$, 此时对偶问题的最优解就是原始问题的最优解.

(2) 如果$d^* = p^*$, 称"强对偶性"成立.

那么如何判断什么时候强对偶性成立呢? 首先, 一般而言, 当原问题是凸优化问题时，强对偶性往往成立 (但并不总是); 否则，可以利用求解对偶问题求出原问题最优值的下界。.

很遗憾, 没有通用的判断条件判断一个问题是否具有强对偶性, 但是很多成果给出了除凸性条件之外的强对偶性成立的条件.

2.3 Slater 条件与 KKT 条件

2.3.1 Slater 条件

Slater 条件用于判断什么情况下强对偶是成立的.

当原始问题为凸优化问题时, 若$\exists x \in \text{relint}(D)$, 使得如下约束条件满足, 则强对偶性成立:

$\begin{array}{ll} f_{i}(x)<0, \quad i=1,2 \ldots, m ; \\ h_{j}(x)=0, \quad j=1,2, \ldots, p \end{array}$

Slater 条件是强对偶性成立的充分不必要条件. 若满足 Slater 条件, 则强对偶一定成立, 不满足时强对偶也可能成立.

2.3.2 KKT 条件

KKT 条件也是强对偶成立的必要条件, 但是某些情况下可以称为充要条件.

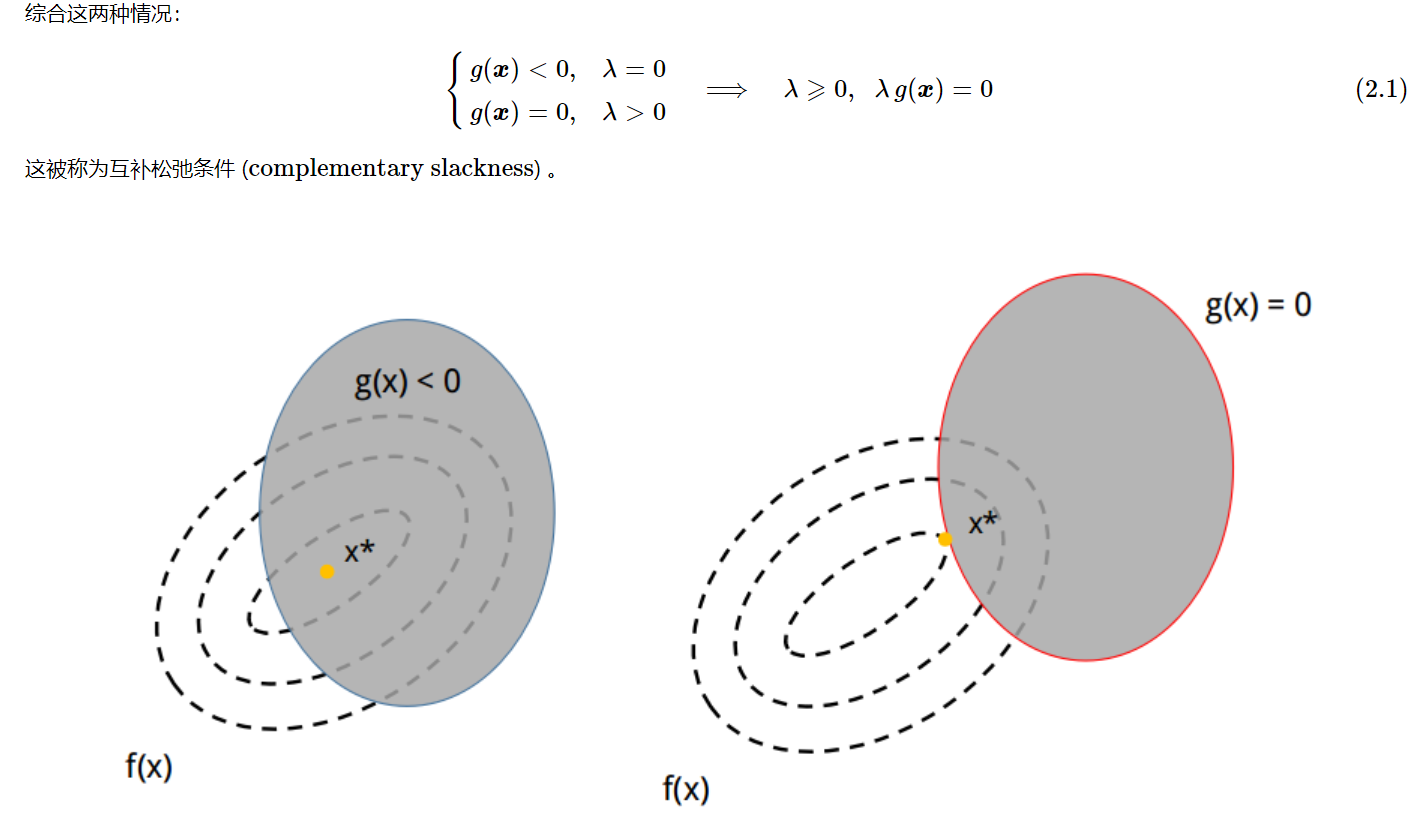
(1) 首先介绍互补松弛条件.

细节可以看 知乎-彭一洋的回答

(2) 下面先介绍必要性.

在对偶间隙为 0 (强对偶成立), 且 $L$ 对 $x$ 可微的前提下，设 $x^{*} ; \lambda^{*}, v^{*}$ 分别是原问题和对偶问题的最优解，则以下四组 KKT 条件必定满足:

$\left\{\begin{array}{ll} \left.\frac{\partial L\left(x, \lambda^{*}, v^{*}\right)}{\partial x}\right|_{x=x^{*}}=0 & (\text { stationarity }) \\ \lambda_{i}^{*} f_{i}\left(x^{*}\right)=0 & (\text { complementary slackness }) \\ f_{i}\left(x^{*}\right) \leq 0, h_{j}\left(x^{*}\right)=0 & (\text { primal feasibility }) \\ \lambda_{i}^{*} \geq 0 & (\text { dual feasibility }) \end{array}\right.$

1. 稳定性条件（stationarity）
   • 该条件是说, 最优值必在极值处取得, 此时$L$关于$x=x^*$的偏导为 0
2. 互补松弛条件（complementary slackness）
   • 互补松弛条件是说, 对于非等式约束而言, 严格不等式是无效的不等式, 需要去掉其影响, 即当$f_{i}\left(x^{*}\right)<0$时, $\lambda_{i}^{*}=0 .$.
   • 而如果约束有效, 必在边界$f_{i}\left(x^{*}\right)=0$上取得, 即当$\lambda_{i}^{*}>0, f_{i}\left(x^{*}\right)=0$
   • 同时表明, 在最优点处，原问题的不等式起作用时, 对偶问题对应的不等式不起作用, 反之亦然.
3. 问题的可行性（primal feasibility）
   • 原问题的最优解必然满足原问题的约束条件。
4. 对偶问题的可行性（dual feasibility）
   • 对偶问题的最优解必然满足对偶问题的约束条件.

对一般的原问题，KKT 条件是$x^{*} ; \lambda^{*}, v^{*}$ 为最优解的必要条件，即只要 $x^{*} ; \lambda^{*}, v^{*}$为最优解，则一定满足 KKT 条件。

(3) 何时时充要条件

若某个凸优化问题具有可微的目标函数和约束函数，且满足 Slater 条件，那么 KKT 条件是最优性的充要条件。

2.4 补充: 原始问题与对偶问题形式

在学习时, 我们经常见到$\min \max$形式的原始问题, 和$\max \min$形式的对偶问题, 这是这么回事呢? 其实时拉格朗日函数的另一种描述方法.

以上就是我们在 SVM 算法里见到的原始问题的形式.

2.5 补充: 拉格朗日对偶方法求解思路

面对一个凸优化问题, 如何使用拉格朗日对偶方法进行求解?:

1. 验证原问题比较难求解, 对偶问题可能会简单一些
   • 要明白, 对偶问题不一定比原问题更简单, 要具体问题具体分析
2. 如果要求原问题最优解, 首先应该验证强对偶性, 说明原问题最优解与对偶问题最优解一致
   • 通过 Convex+slater 条件验证强对偶性
   • 对于 Convex + 可微 的问题, KKT 条件 $\Rightarrow$ 强对偶 + 最优解
3. 写出对偶问题
4. 首先将$\lambda,v$看作常数, 对原始问题关于$x$求导置零, 得到 x 关于$\lambda,v$的表示, 带入对偶问题, 得到对偶函数.
5. 求解对偶问题的最优解, 得到$\lambda^*,v^*$
6. 由 KKT 条件, 倒推出$x^*$

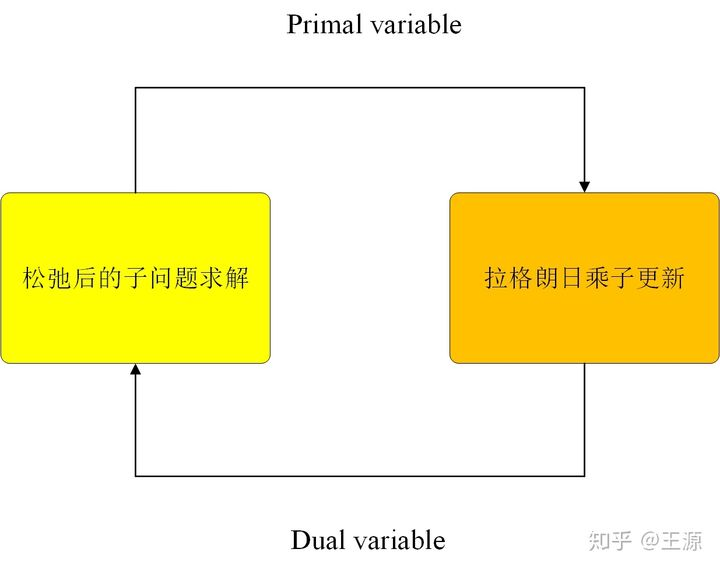
2.5 补充: 整数规划中的拉格朗日松弛方法

一般过程为,

• 首先求出松弛后的子问题, 并对其进行快速求解;
• 注意此时对偶问题是一个非光滑(分段)凸优化问题, 可以使用次梯度法求解
• 之后进行迭代优化.

2.3 小结

1. 至此, 我们总结一下使用拉格朗日对偶问题带来哪些便利呢?

2. 将原始困难的约束转为容易求解的问题.

3. 约束减少了，对偶问题只剩 n 个不等式约束
4. 基于上下界的方法可以很好地帮助分析原始问题的性质.
5. 主问题不一定是凸优化问题, 对偶问题一定是凸优化问题
6. 如果强对偶性成立, 则对偶问题的最优解等于原始问题的最优解.

7. 原问题是凸优化问题时，强对偶性往往成立 (并不总是); 否则，可以利用求解对偶问题求出原问题最优值的下界。

8. 几种条件和强对偶的关系

9. 对于任意问题, 强对偶 + 最优解 $\Rightarrow$ KKT 条件

10. 对于 Convex + 可微 的问题, KKT 条件 $\Rightarrow$ 强对偶 + 最优解
11. Convex + Slater $\Rightarrow$ 强对偶

3 例子 SVM

可以直接看《统计学习方法》第 7 章的内容

总结

1. 通过具体问题， 引出拉格朗日乘子法

   • 使用拉格朗日松弛, 可以把问题进行分解， （整数规划）
   • 作拉格朗日松弛并不是要把所有约束都放到目标函数上去的, 而是有选择性的对约束进行处理.如何区分难的约束主要依靠个人经验判断. 但是, 一般而言, 选择 linked/coupling constraints, 可以让不可分的问题分解为简单的子问题.
   • 针对不同的约束， 如何选择乘子$\lambda$, 令松弛后的问题， 在违反约束时给出恰当的惩罚

2. 拉格朗日函数给出了原始问题的一个下界函数。

   • 分析“界”是一种重要的数学分析方法

3. 拉格朗日对偶函数--下确界

4. 之后通过分析对偶问题最优解与原始问题最优解的关系， --强、弱对偶
5. 最后通过 slater 条件和 KKT 条件，讨论最优解与强对偶的关系， 以及通过对偶求解原始问题最优解的过程.

注意， 并不是对偶问题不一定比原始问题容易， 还是需要经验判断的。

参考:

• https://www.zhihu.com/question/58584814/answer/159863739
• https://zhuanlan.zhihu.com/p/103961917
• 拉格朗日对偶性
• https://zhuanlan.zhihu.com/p/145944142
• 孙小玲-整数规划
• 李航- 统计学习方法